| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
Let’s use the General Strategy for Solving Linear Equations introduced earlier to solve the equation
|
| |
| To isolate the term, subtract from both sides. |
|
| Simplify the left side. |
|
| Change the constants to equivalent fractions with the LCD. |
|
| Subtract. |
|
| Multiply both sides by the reciprocal of . |
|
| Divide. |
|
| Simplify. |
|
This method worked fine, but many students don’t feel very confident when they see all those fractions. So we are going to show an alternate method to solve equations with fractions. This alternate method eliminates the fractions.
We will apply the Multiplication Property of Equality and multiply both sides of an equation by the least common denominator of all the fractions in the equation. The result of this operation will be a new equation, equivalent to the first, but with no fractions. This process is called clearing the equation of fractions . Let’s solve the same equation again, but this time use the method that clears the fractions.
Solve:
| Find the least common denominator of all the fractions in the equation. |
|
| Multiply both sides of the equation by that LCD, 8. This clears the fractions. |
|
| Use the Distributive Property. |
|
| Simplify — and notice, no more fractions! |
|
| Solve using the General Strategy for Solving Linear Equations. |
|
| Simplify. |
|
Check: Let
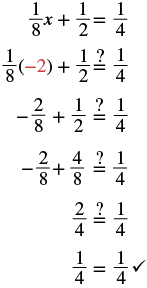 |
Notice in [link] that once we cleared the equation of fractions, the equation was like those we solved earlier in this chapter. We changed the problem to one we already knew how to solve! We then used the General Strategy for Solving Linear Equations.
Solve:
We want to clear the fractions by multiplying both sides of the equation by the LCD of all the fractions in the equation.
| Find the least common denominator of all the fractions in the equation. |
|
| Multiply both sides of the equation by 12. |
|
| Distribute. |
|
| Simplify — and notice, no more fractions! |
|
| Combine like terms. |
|
| Divide by 7. |
|
| Simplify. |
|
| Check: Let | |
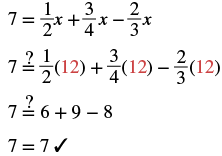 |
In the next example, we’ll have variables and fractions on both sides of the equation.
Solve:
| Find the LCD of all the fractions in the equation. |
|
| Multiply both sides by the LCD. |
|
| Distribute. |
|
| Simplify — no more fractions! |
|
| Subtract from both sides. |
|
| Simplify. |
|
| Subtract 2 from both sides. |
|
| Simplify. |
|
| Divide by 5. |
|
| Simplify. |
|
| Check: Substitute | |
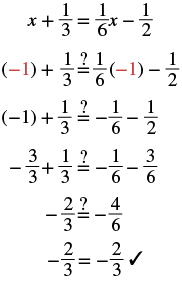 |

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?