8.4 Relative strengths of acids and bases  (Page 26/18)

We can rank the strengths of acids by the extent to which they ionize in aqueous solution. The reaction of an acid with water is given by the general expression:

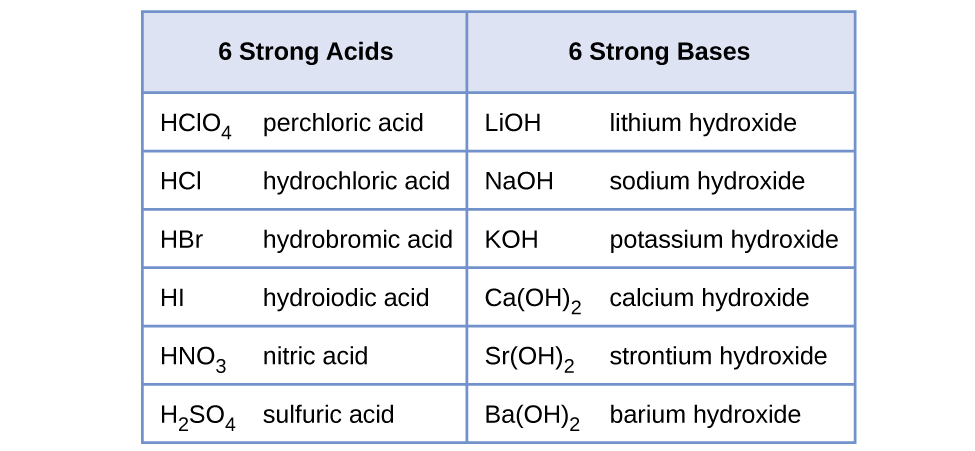
Water is the base that reacts with the acid HA, A ⁻ is the conjugate base of the acid HA, and the hydronium ion is the conjugate acid of water. A strong acid yields 100% (or very nearly so) of ${\text{H}}_3{\text{O}}^{\text{+}}$ and A ⁻ when the acid ionizes in water; [link] lists several strong acids. A weak acid gives small amounts of ${\text{H}}_3{\text{O}}^{\text{+}}$ and A ⁻ .

The relative strengths of acids may be determined by measuring their equilibrium constants in aqueous solutions. In solutions of the same concentration, stronger acids ionize to a greater extent, and so yield higher concentrations of hydronium ions than do weaker acids. The equilibrium constant for an acid is called the acid-ionization constant, K _a . For the reaction of an acid HA:

we write the equation for the ionization constant as:

where the concentrations are those at equilibrium. Although water is a reactant in the reaction, it is the solvent as well, so we do not include [H ₂ O] in the equation. The larger the K _a of an acid, the larger the concentration of ${\text{H}}_3{\text{O}}^{\text{+}}$ and A ⁻ relative to the concentration of the nonionized acid, HA. Thus a stronger acid has a larger ionization constant than does a weaker acid. The ionization constants increase as the strengths of the acids increase. (A table of ionization constants of weak acids appears in Appendix H , with a partial listing in [link] .)

The following data on acid-ionization constants indicate the order of acid strength CH ₃ CO ₂ H<HNO ₂ < ${\text{HSO}}_4{}^{\text{−}}:$

Another measure of the strength of an acid is its percent ionization. The percent ionization    of a weak acid is the ratio of the concentration of the ionized acid to the initial acid concentration, times 100:

Because the ratio includes the initial concentration, the percent ionization for a solution of a given weak acid varies depending on the original concentration of the acid, and actually decreases with increasing acid concentration.