| << Chapter < Page | Chapter >> Page > |
A deep-sea fisherman hooks a big fish that swims away from the boat pulling the fishing line from his fishing reel. The whole system is initially at rest and the fishing line unwinds from the reel at a radius of 4.50 cm from its axis of rotation. The reel is given an angular acceleration of for 2.00 s as seen in [link] .
(a) What is the final angular velocity of the reel?
(b) At what speed is fishing line leaving the reel after 2.00 s elapses?
(c) How many revolutions does the reel make?
(d) How many meters of fishing line come off the reel in this time?
Strategy
In each part of this example, the strategy is the same as it was for solving problems in linear kinematics. In particular, known values are identified and a relationship is then sought that can be used to solve for the unknown.
Solution for (a)
Here and are given and needs to be determined. The most straightforward equation to use is because the unknown is already on one side and all other terms are known. That equation states that
We are also given that (it starts from rest), so that
Solution for (b)
Now that is known, the speed can most easily be found using the relationship
where the radius of the reel is given to be 4.50 cm; thus,
Note again that radians must always be used in any calculation relating linear and angular quantities. Also, because radians are dimensionless, we have .
Solution for (c)
Here, we are asked to find the number of revolutions. Because , we can find the number of revolutions by finding in radians. We are given and , and we know is zero, so that can be obtained using .
Converting radians to revolutions gives
Solution for (d)
The number of meters of fishing line is , which can be obtained through its relationship with :
Discussion
This example illustrates that relationships among rotational quantities are highly analogous to those among linear quantities. We also see in this example how linear and rotational quantities are connected. The answers to the questions are realistic. After unwinding for two seconds, the reel is found to spin at 220 rad/s, which is 2100 rpm. (No wonder reels sometimes make high-pitched sounds.) The amount of fishing line played out is 9.90 m, about right for when the big fish bites.
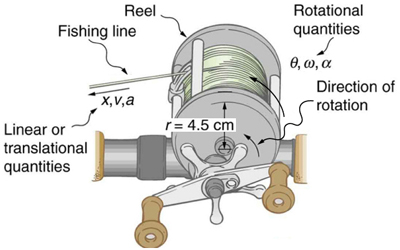
Now let us consider what happens if the fisherman applies a brake to the spinning reel, achieving an angular acceleration of . How long does it take the reel to come to a stop?
Strategy
We are asked to find the time for the reel to come to a stop. The initial and final conditions are different from those in the previous problem, which involved the same fishing reel. Now we see that the initial angular velocity is and the final angular velocity is zero. The angular acceleration is given to be . Examining the available equations, we see all quantities but t are known in making it easiest to use this equation.
Solution
The equation states
We solve the equation algebraically for t , and then substitute the known values as usual, yielding
Discussion
Note that care must be taken with the signs that indicate the directions of various quantities. Also, note that the time to stop the reel is fairly small because the acceleration is rather large. Fishing lines sometimes snap because of the accelerations involved, and fishermen often let the fish swim for a while before applying brakes on the reel. A tired fish will be slower, requiring a smaller acceleration.

Notification Switch
Would you like to follow the 'Introduction to applied math and physics' conversation and receive update notifications?