8.2 Centripetal force  (Page 3/10)

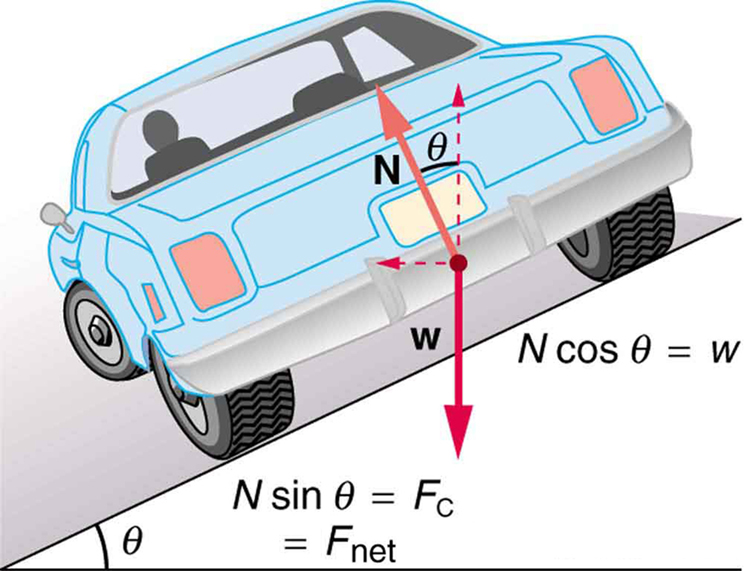
Because the car does not leave the surface of the road, the net vertical force must be zero, meaning that the vertical components of the two external forces must be equal in magnitude and opposite in direction. From the figure, we see that the vertical component of the normal force is $N\text{cos}\theta$ , and the only other vertical force is the car’s weight. These must be equal in magnitude; thus,

Now we can combine the last two equations to eliminate $N$ and get an expression for $\theta$ , as desired. Solving the second equation for $N=\text{mg}/(\text{cos}\theta )$ , and substituting this into the first yields

Taking the inverse tangent gives

This expression can be understood by considering how $\theta$ depends on $v$ and $r$ . A large $\theta$ will be obtained for a large $v$ and a small $r$ . That is, roads must be steeply banked for high speeds and sharp curves. Friction helps, because it allows you to take the curve at greater or lower speed than if the curve is frictionless. Note that $\theta$ does not depend on the mass of the vehicle.

Phet explorations: gravity and orbits

Move the sun, earth, moon and space station to see how it affects their gravitational forces and orbital paths. Visualize the sizes and distances between different heavenly bodies, and turn off gravity to see what would happen without it!

Section summary

• Centripetal force ${\text{F}}_{\text{c}}$ is any force causing uniform circular motion. It is a “center-seeking” force that always points toward the center of rotation. It is perpendicular to linear velocity $v$ and has magnitude
  $F_{\text{c}}={\text{ma}}_{\text{c}}\text{,}$

  which can also be expressed as

  $\left(\begin{array}{c}{F}_{\text{c}}=m\frac{v^2}{r}\\ \begin{array}{}\text{or}\\ F_{\text{c}}=\text{mr}{\omega }^2\end{array}\end{array},\right\}$