| << Chapter < Page | Chapter >> Page > |
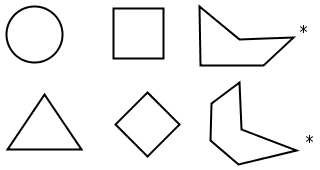
If you take some lines and join them such that the end point of the first line meets the starting point of the last line, you will get a polygon . Each line that makes up the polygon is known as a side . A polygon has interior angles. These are the angles that are inside the polygon. The number of sides of a polygon equals the number of interior angles. If a polygon has equal length sides and equal interior angles, then the polygon is called a regular polygon . Some examples of polygons are shown in [link] .
A triangle is a three-sided polygon. Triangles are usually split into three categories: equilateral, isosceles, and scalene, depending on how many of the sides are of equal length. A fourth category, right-angled triangle (or simply 'right triangle') is used to refer to triangles with one right angle. Note that all right-angled triangles are also either isosceles (if the other two sides are equal) or scalene (it should be clear why you cannot have an equilateral right triangle!). The properties of these triangles are summarised in [link] .
| Name | Diagram | Properties |
| equilateral |
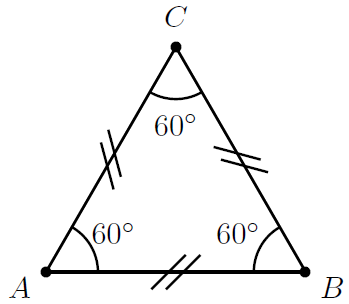 |
All three sides are equal in length (denoted by the short lines drawn through all the sides of equal length) and all three angles are equal. |
| isosceles |
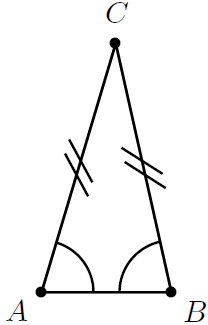 |
Two sides are equal in length. The angles opposite the equal sides are equal. |
| right-angled |
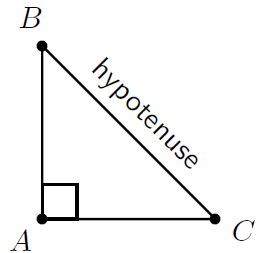 |
This triangle has one right angle. The side opposite this angle is called the hypotenuse . |
| scalene (non-syllabus) |
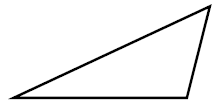 |
All sides and angles are different. |
We use the notation to refer to a triangle with corners labeled , , and .


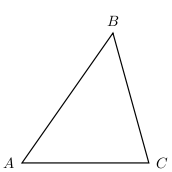

Two triangles are called congruent if one of them can be superimposed, that is moved on top of to exactly cover, the other. In other words, if both triangles have all of the same angles and sides, then they are called congruent. To decide whether two triangles are congruent, it is not necessary to check every side and angle. The following list describes various requirements that are sufficient to know when two triangles are congruent.
| Label | Description | Diagram |
| RHS | If the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and the respective side of another triangle, then the triangles are congruent. |
 |
| SSS | If three sides of a triangle are equal in length to the same sides of another triangle, then the two triangles are congruent |
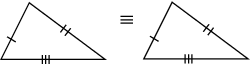 |
| SAS | If two sides and the included angle of one triangle are equal to the same two sides and included angle of another triangle, then the two triangles are congruent. |
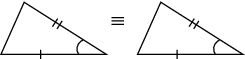 |
| AAS | If one side and two angles of one triangle are equal to the same one side and two angles of another triangle, then the two triangles are congruent. |
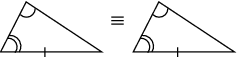 |

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [caps]' conversation and receive update notifications?