8.1 Confidence intervals for a population mean, population standard  (Page 8/7)

Calculating the confidence interval

To construct a confidence interval for a single unknown population mean $\mu$ , where the population standard deviation is known, we need $\overline{x}$ as an estimate for $\mu$ and we need the margin of error. Here, the margin of error is called the error bound for a population mean (abbreviated EBM ). The sample mean $\overline{x}$ is the point estimate of the unknown population mean $\mu$

The confidence interval estimate will have the form:

• (point estimate - error bound, point estimate + error bound) or, in symbols, $(\overline{x}-\mathrm{EBM},\overline{x}+\mathrm{EBM})$

The margin of error depends on the confidence level (abbreviated CL ). The confidence level is the probability that the confidence interval estimate that we will calculate will contain the true population parameter. Most often, itis the choice of the person constructing the confidence interval to choose a confidence level of 90% or higher because he wants to be reasonably certain of hisconclusions.

There is another probability called alpha ( $\alpha$ ). $\alpha$ is related to the confidence level CL. $\alpha$ is the probability that the sample produced a point estimate that is not within the appropriate margin of error of the unknown population parameter.

A confidence interval for a population mean with a known standard deviation is based on the fact that the sample means follow an approximately normaldistribution. Suppose that our sample has a mean of $\overline{x}=10$ and we have constructed the 90% confidence interval (5, 15)where $\text{EBM}=5$ .

To get a 90% confidence interval, we must include the central 90% of the probability of the normal distribution. If we include the central 90%, we leave out a total of 10% in both tails, or 5% in each tail, of the normal distribution.

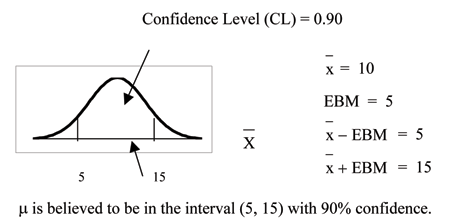
To capture the central 90%, we must go out 1.645 "standard deviations" on either side of the calculated sample mean. 1.645 is the z-score from a Standard Normalprobability distribution that puts an area of 0.90 in the center, an area of 0.05 in the far left tail, and an area of 0.05 in the far right tail.