7.8 Entropy and the second law of thermodynamics: disorder and the  (Page 2/6)

With respect to entropy, there are only two possibilities: entropy is constant for a reversible process, and it increases for an irreversible process. There is a fourth version of the second law of thermodynamics stated in terms of entropy :

The total entropy of a system either increases or remains constant in any process; it never decreases.

For example, heat transfer cannot occur spontaneously from cold to hot, because entropy would decrease.

Entropy is very different from energy. Entropy is not conserved but increases in all real processes. Reversible processes are the processes in which the most heat transfer to work takes place and are also the ones that keep entropy constant. Thus we are led to make a connection between entropy and the availability of energy to do work.

Entropy and the unavailability of energy to do work

What does a change in entropy mean, and why should we be interested in it? One reason is that entropy is directly related to the fact that not all heat transfer can be converted into work. When entropy increases, a certain amount of energy becomes permanently unavailable to do work. The energy is not lost, but its character is changed, so that some of it can never be converted to doing work—that is, to an organized force acting through a distance.

Order to disorder

Entropy is related not only to the unavailability of energy to do work—it is also a measure of disorder. This notion was initially postulated by Ludwig Boltzmann in the 1800s. For example, melting a block of ice means taking a highly structured and orderly system of water molecules and converting it into a disorderly liquid in which molecules have no fixed positions. (See [link] .) There is a large increase in entropy in the process, as seen in the following example.

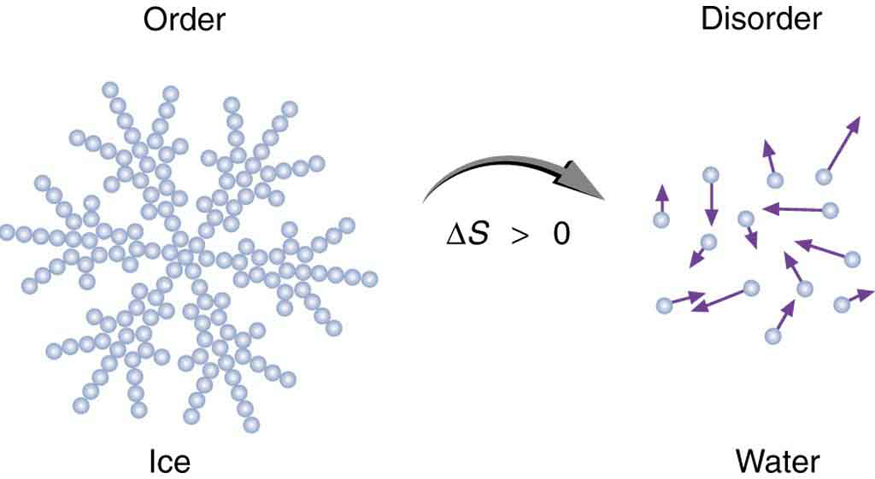
In another easily imagined example, suppose we mix equal masses of water originally at two different temperatures, say $\text{20.0º C}$ and $\text{40.0º C}$ . The result is water at an intermediate temperature of $\text{30.0º C}$ . Three outcomes have resulted: entropy has increased, some energy has become unavailable to do work, and the system has become less orderly. Let us think about each of these results.