7.7 Practice 3: confidence intervals for proportions

What is being counted?

In words, define the Random Variable $X$ . $X=$

Calculate the following:

• a $x=$
• b $n=$
• c $p\text{'}=$

State the estimated distribution of $X$ . $X$ ~

Define a new Random Variable $P\text{'}$ . What is $p\text{'}$ estimating?

In words, define the Random Variable $P\text{'}$ . $P\text{'}=$

State the estimated distribution of $P\text{'}$ . $P\text{'}$ ~

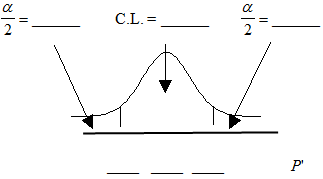
How much area is in both tails (combined)? $\alpha =$

How much area is in each tail? $\frac{\alpha }{2}=$

Calculate the following:

• a lower limit =
• b upper limit =
• c error bound =

The 92% Confidence Interval is:

In one complete sentence, explain what the interval means.

Using the same $p\text{'}$ and level of confidence, suppose that n were increased to 100. Would the error bound become larger or smaller? How do you know?

Using the same $p\text{'}$ and $n=\text{80}$ , how would the error bound change if the confidence level were increased to 98%? Why?

If you decreased the allowable error bound, why would the minimum sample size increase (keeping the same level of confidence)?