| << Chapter < Page | Chapter >> Page > |
In this module, we will learn about work and energy associated with rotational motion. [link] shows a worker using an electric grindstone propelled by a motor. Sparks are flying, and noise and vibration are created as layers of steel are pared from the pole. The stone continues to turn even after the motor is turned off, but it is eventually brought to a stop by friction. Clearly, the motor had to work to get the stone spinning. This work went into heat, light, sound, vibration, and considerable rotational kinetic energy .

Work must be done to rotate objects such as grindstones or merry-go-rounds. Work was defined in Uniform Circular Motion and Gravitation for translational motion, and we can build on that knowledge when considering work done in rotational motion. The simplest rotational situation is one in which the net force is exerted perpendicular to the radius of a disk (as shown in [link] ) and remains perpendicular as the disk starts to rotate. The force is parallel to the displacement, and so the net work done is the product of the force times the arc length traveled:
To get torque and other rotational quantities into the equation, we multiply and divide the right-hand side of the equation by , and gather terms:
We recognize that and , so that
This equation is the expression for rotational work. It is very similar to the familiar definition of translational work as force multiplied by distance. Here, torque is analogous to force, and angle is analogous to distance. The equation is valid in general, even though it was derived for a special case.
To get an expression for rotational kinetic energy, we must again perform some algebraic manipulations. The first step is to note that , so that
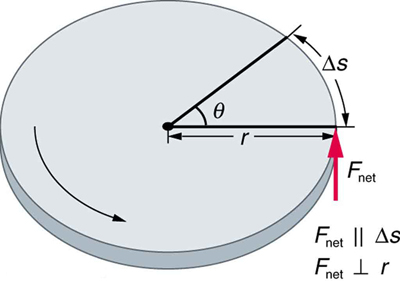
Work and energy in rotational motion are completely analogous to work and energy in translational motion, first presented in Uniform Circular Motion and Gravitation .
Now, we solve one of the rotational kinematics equations for . We start with the equation
Next, we solve for :
Substituting this into the equation for net and gathering terms yields
This equation is the work-energy theorem for rotational motion only. As you may recall, net work changes the kinetic energy of a system. Through an analogy with translational motion, we define the term to be rotational kinetic energy for an object with a moment of inertia and an angular velocity :

Notification Switch
Would you like to follow the 'College physics arranged for cpslo phys141' conversation and receive update notifications?