7.5 Inelastic collisions in one dimension  (Page 16/7)

We have seen that in an elastic collision, internal kinetic energy is conserved. An inelastic collision    is one in which the internal kinetic energy changes (it is not conserved). This lack of conservation means that the forces between colliding objects may remove or add internal kinetic energy. Work done by internal forces may change the forms of energy within a system. For inelastic collisions, such as when colliding objects stick together, this internal work may transform some internal kinetic energy into heat transfer. Or it may convert stored energy into internal kinetic energy, such as when exploding bolts separate a satellite from its launch vehicle.

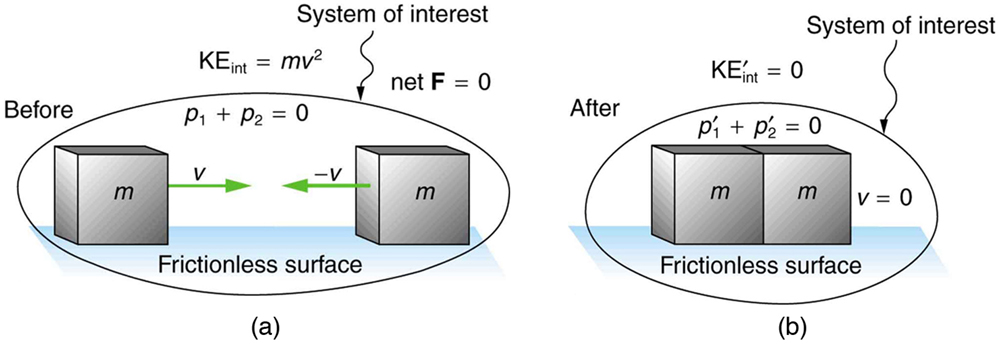
[link] shows an example of an inelastic collision. Two objects that have equal masses head toward one another at equal speeds and then stick together. Their total internal kinetic energy is initially ${\text{mv}}^2\left(\frac{1}{2}{\text{mv}}^2+\frac{1}{2}{\text{mv}}^2\right)$ . The two objects come to rest after sticking together, conserving momentum. But the internal kinetic energy is zero after the collision. A collision in which the objects stick together is sometimes called a perfectly inelastic collision    because it reduces internal kinetic energy more than does any other type of inelastic collision. In fact, such a collision reduces internal kinetic energy to the minimum it can have while still conserving momentum.

Calculating velocity and change in kinetic energy: inelastic collision of a puck and a goalie

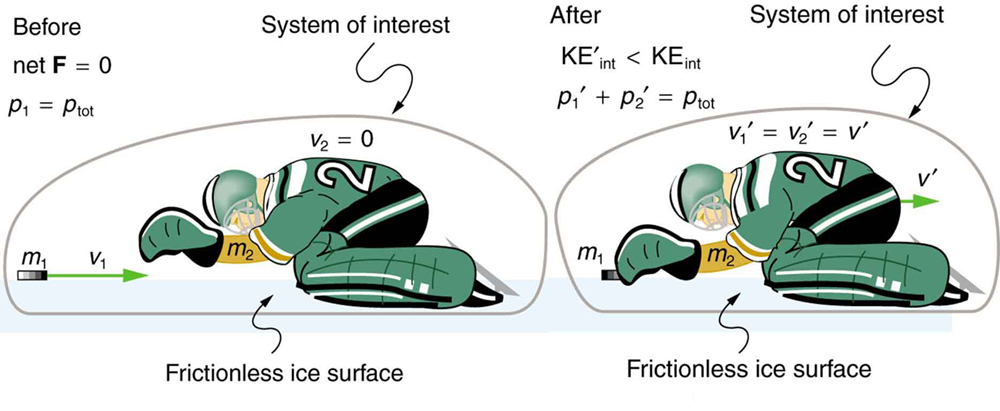
(a) Find the recoil velocity of a 70.0-kg ice hockey goalie, originally at rest, who catches a 0.150-kg hockey puck slapped at him at a velocity of 35.0 m/s. (b) How much kinetic energy is lost during the collision? Assume friction between the ice and the puck-goalie system is negligible. (See [link] )

Strategy

Momentum is conserved because the net external force on the puck-goalie system is zero. We can thus use conservation of momentum to find the final velocity of the puck and goalie system. Note that the initial velocity of the goalie is zero and that the final velocity of the puck and goalie are the same. Once the final velocity is found, the kinetic energies can be calculated before and after the collision and compared as requested.