7.5 Imaginary concepts -- extra for experts

Illegal operations

So far, we have seen three different illegal operations in math.

1. You cannot take the square root of a negative number. (Hence, the domain of $\sqrt{x}$ is $x\ge 0$ .)
2. You cannot divide by zero. (Hence, the domain of $\frac{1}{x}$ is $x\ne 0$ .)
3. You cannot take the log of 0 or a negative number. (Hence, the domain of $\text{log}\left(x\right)$ is $x>0$ .)

Imaginary numbers give us a way of violating the first restriction. Less obviously, they also give us a way of violating the third restriction: with imaginary numbers, you can take the log of a negative number.

So, how about that second restriction? Do you ever reach a point in math where the teacher admits “OK, we really can divide by 0 now”? Can we define a new imaginary number $j=\frac{1}{0}$ ?

The answer is emphatically no: you really can’t divide by 0 . If you attempt to define an imaginary way around this problem, all of math breaks down. Consider the following simple example:

You see? Dividing by 0 takes us from true conclusions to false ones.

The astonishing thing about the definition $i=$ $\sqrt{-1}$ is that, although it is imaginary and nonsensical, it is consistent: it does not lead to any logical contradictions. You can find many ways to simplify $\frac{1}{i}$ and it will always reduce to $\mathrm{–i}$ in the end. Division by zero can never be consistent in this way, so it is always forbidden.

A great deal of Calculus is concerned with getting around this problem, by dividing by numbers that are very close to zero.

The world of numbers

When you first learn about numbers, you learn the counting numbers:

These numbers are perfect for answering questions such as “How many sticks do I have?” “How many days until Christmas?” “How many years old are you?”

For other questions, however, you run into limitations. In measuring temperature, for instance, we find that we need lower numbers than 1. Hence, we arrive at a broader list:

The addition of 0 and the negative numbers gives us a new, broader set. The original idea of numbers is now seen as a special case of this more general idea; the original set is a subset of this one.

Still, if we are measuring lengths of sticks, we will find that often they fall between our numbers. Now we have to add fractions, or decimals, to create the set of rational numbers . I can no longer list the set, but I can give examples.

The word “rational” implies a ratio , or fraction: the ratio of two integers . Hence, we define our new, broader set (rational numbers) in terms of our older, more limited set (integers). Rational numbers can be expressed as either fractions, or as decimals (which either end after a certain number of digits, or repeat the same loop of digits forever).

This set seems to be all-inclusive, but it isn’t: certain numbers cannot be expressed in this form.

The square root of any non-perfect square is “irrational” and so is $\pi$ . They can be approximated as fractions, but not expressed exactly. As decimals, they go on forever but do not endlessly repeat the same loop.

If you take the rationals and irrationals together, you get the real numbers . The real numbers are all the numbers represented on a number line.

Now, with this unit, we have added the final piece of the puzzle, the complex numbers . A complex number is any number $a+\mathrm{bi}$ where $a$ and $b$ are real numbers. Hence, just as our definition of rational numbers was based on our definition of integers, so our definition of complex numbers is based on our definition of real numbers. And of course, if $b=0$ then we have a real number: the old set is a subset of the new.

All of this can be represented in the following diagram.

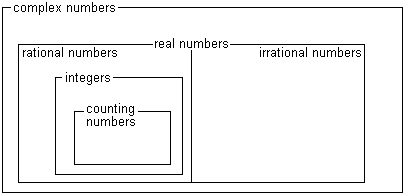
The diagram captures the vital idea of subsets: all real numbers are complex numbers, but not all complex numbers are real.

Similarly, the diagram shows that if you take all the rational numbers, and all the irrational numbers, together they make up the set of real numbers.