7.4 Nonconservative forces

Nonconservative forces and friction

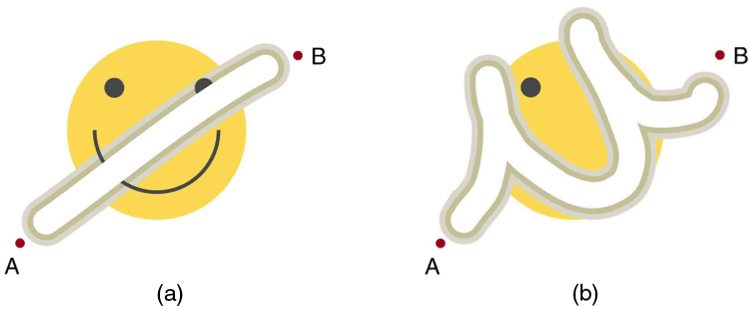
Forces are either conservative or nonconservative. Conservative forces were discussed in Conservative Forces and Potential Energy . A nonconservative force    is one for which work depends on the path taken. Friction is a good example of a nonconservative force. As illustrated in [link] , work done against friction depends on the length of the path between the starting and ending points. Because of this dependence on path, there is no potential energy associated with nonconservative forces. An important characteristic is that the work done by a nonconservative force adds or removes mechanical energy from a system . Friction , for example, creates thermal energy that dissipates, removing energy from the system. Furthermore, even if the thermal energy is retained or captured, it cannot be fully converted back to work, so it is lost or not recoverable in that sense as well.

How nonconservative forces affect mechanical energy

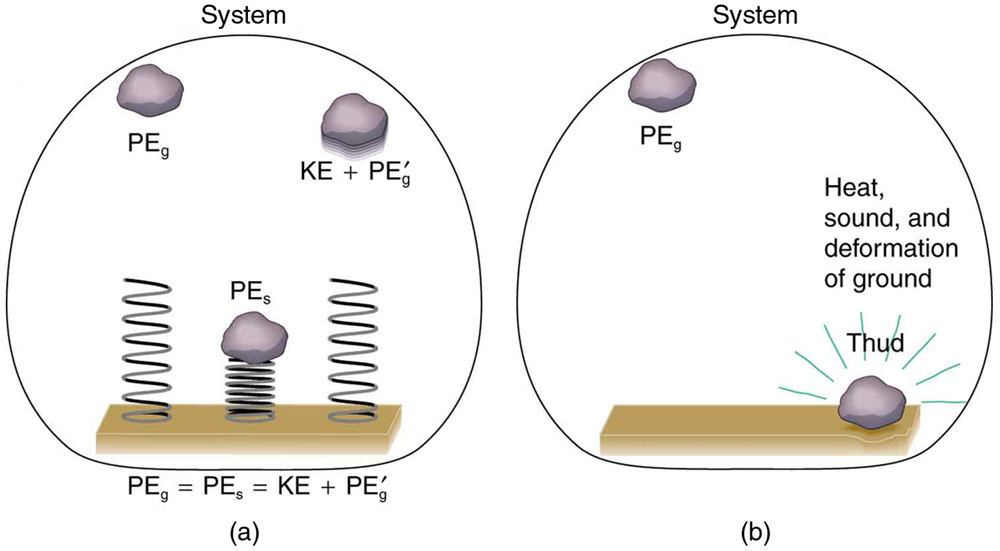
Mechanical energy may not be conserved when nonconservative forces act. For example, when a car is brought to a stop by friction on level ground, it loses kinetic energy, which is dissipated as thermal energy, reducing its mechanical energy. [link] compares the effects of conservative and nonconservative forces. We often choose to understand simpler systems such as that described in [link] (a) first before studying more complicated systems as in [link] (b).

How the work-energy theorem applies

Now let us consider what form the work-energy theorem takes when both conservative and nonconservative forces act. We will see that the work done by nonconservative forces equals the change in the mechanical energy of a system. As noted in Kinetic Energy and the Work-Energy Theorem , the work-energy theorem states that the net work on a system equals the change in its kinetic energy, or $W_{\text{net}}=\text{ΔKE}$ . The net work is the sum of the work by nonconservative forces plus the work by conservative forces. That is,