| << Chapter < Page | Chapter >> Page > |
Rewrite the equation in rectangular coordinates and identify its graph.
which is the equation of a parabola opening upward.
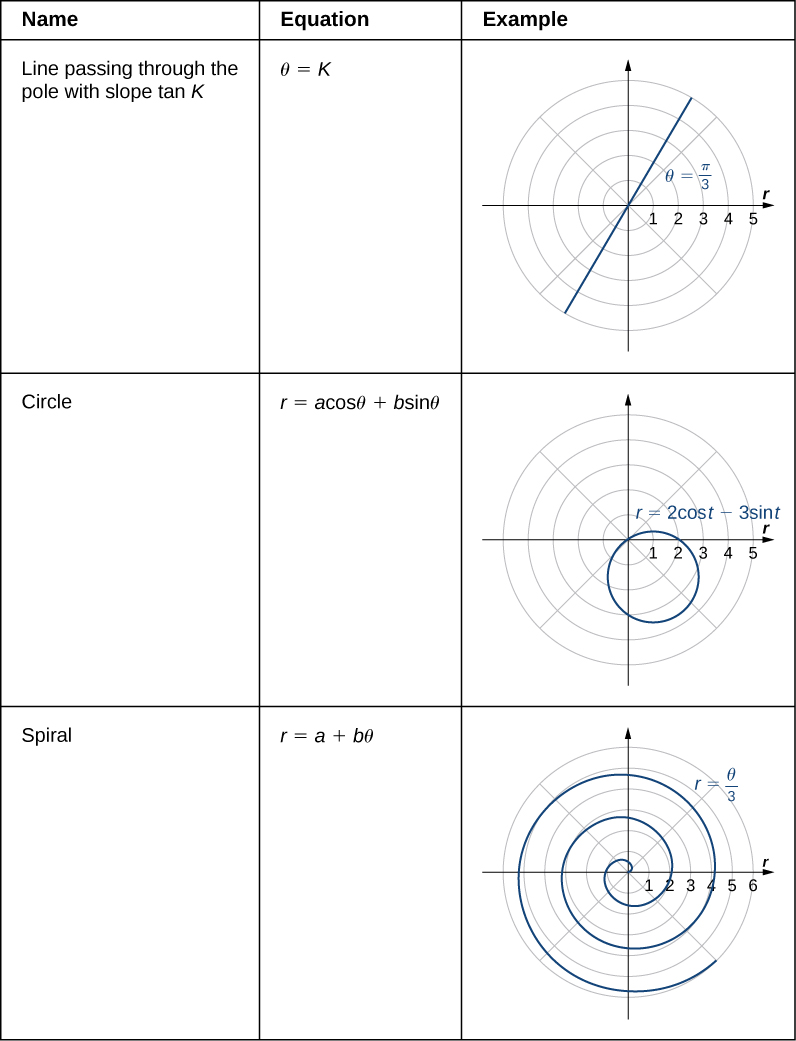
We have now seen several examples of drawing graphs of curves defined by polar equations . A summary of some common curves is given in the tables below. In each equation, a and b are arbitrary constants.
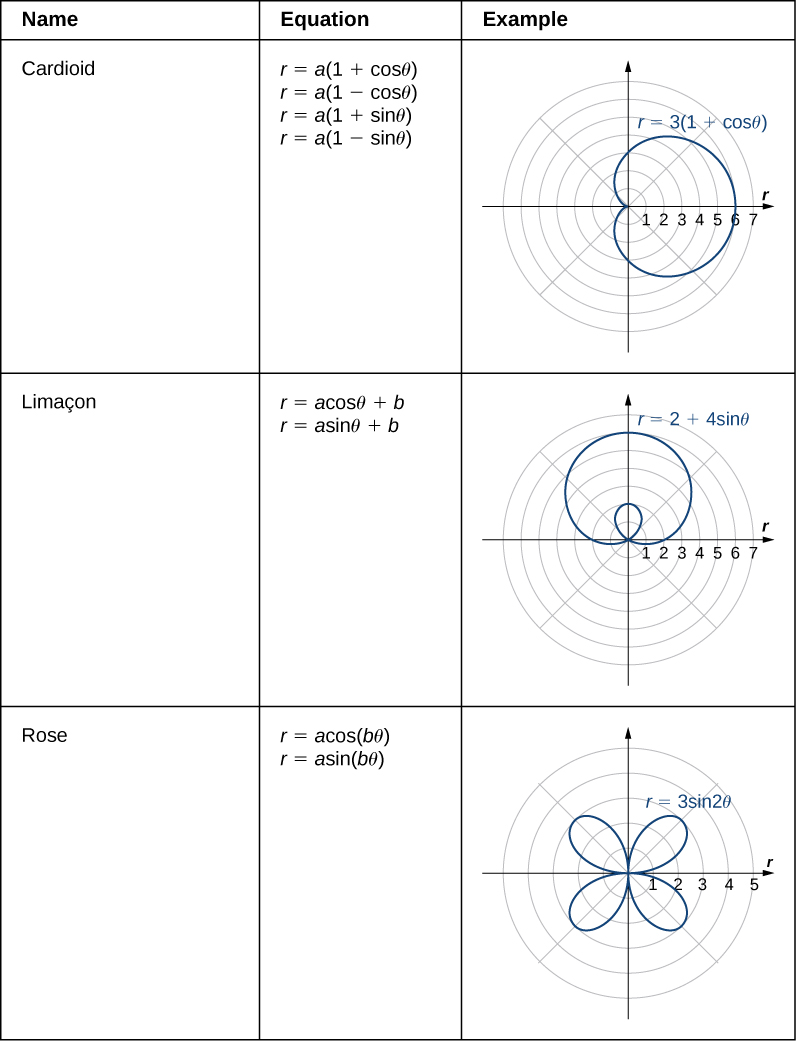
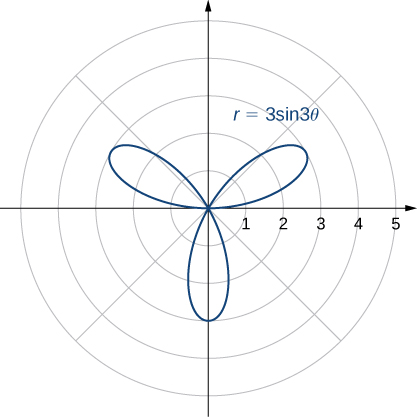
A cardioid is a special case of a limaçon (pronounced “lee-mah-son”), in which or The rose is a very interesting curve. Notice that the graph of has four petals. However, the graph of has three petals as shown.
If the coefficient of is even, the graph has twice as many petals as the coefficient. If the coefficient of is odd, then the number of petals equals the coefficient. You are encouraged to explore why this happens. Even more interesting graphs emerge when the coefficient of is not an integer. For example, if it is rational, then the curve is closed; that is, it eventually ends where it started ( [link] (a)). However, if the coefficient is irrational, then the curve never closes ( [link] (b)). Although it may appear that the curve is closed, a closer examination reveals that the petals just above the positive x axis are slightly thicker. This is because the petal does not quite match up with the starting point.
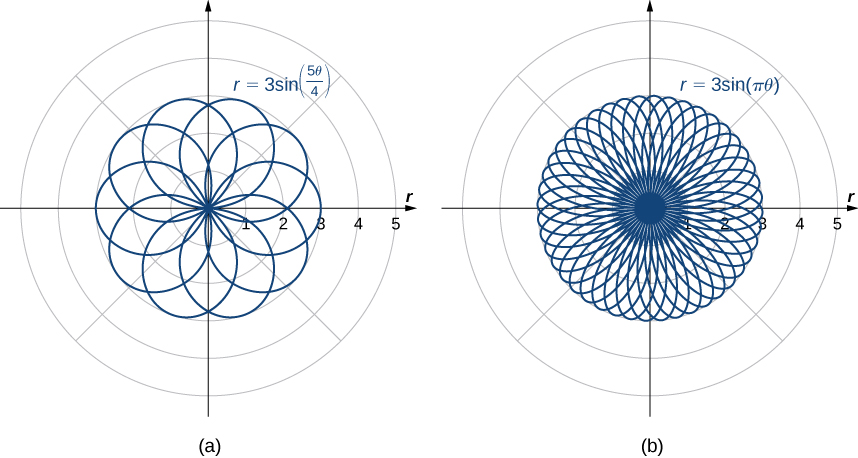
Since the curve defined by the graph of never closes, the curve depicted in [link] (b) is only a partial depiction. In fact, this is an example of a space-filling curve . A space-filling curve is one that in fact occupies a two-dimensional subset of the real plane. In this case the curve occupies the circle of radius 3 centered at the origin.
Recall the chambered nautilus introduced in the chapter opener. This creature displays a spiral when half the outer shell is cut away. It is possible to describe a spiral using rectangular coordinates. [link] shows a spiral in rectangular coordinates. How can we describe this curve mathematically?
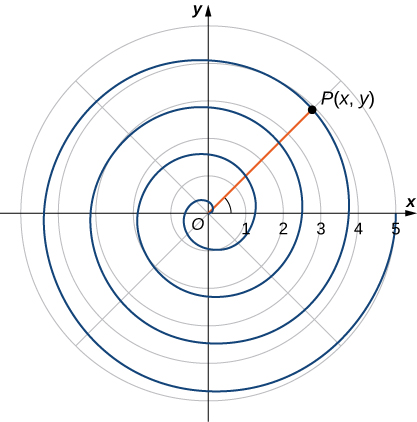
As the point P travels around the spiral in a counterclockwise direction, its distance d from the origin increases. Assume that the distance d is a constant multiple k of the angle that the line segment OP makes with the positive x -axis. Therefore where is the origin. Now use the distance formula and some trigonometry:
Although this equation describes the spiral, it is not possible to solve it directly for either x or y . However, if we use polar coordinates, the equation becomes much simpler. In particular, and is the second coordinate. Therefore the equation for the spiral becomes Note that when we also have so the spiral emanates from the origin. We can remove this restriction by adding a constant to the equation. Then the equation for the spiral becomes for arbitrary constants and This is referred to as an Archimedean spiral , after the Greek mathematician Archimedes.
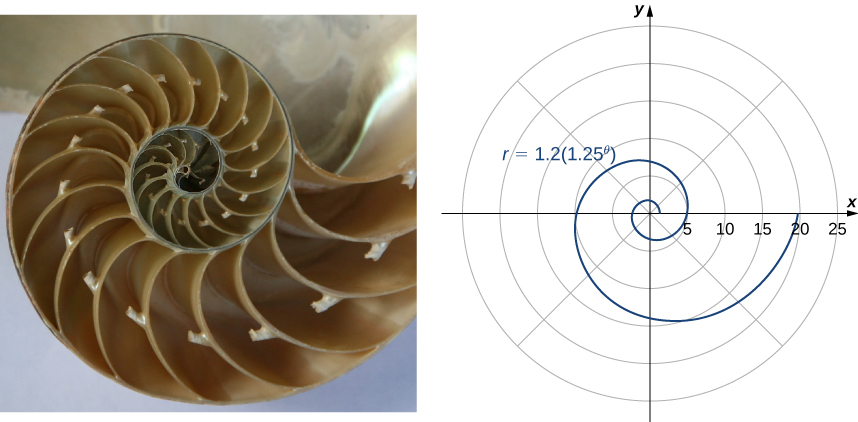
Another type of spiral is the logarithmic spiral, described by the function A graph of the function is given in [link] . This spiral describes the shell shape of the chambered nautilus.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?