1. Home
  2. Ut austin - principles of
  3. Chemical equilibria
  4. Equilibrium calculations

7.3 Equilibrium calculations  (Page 6/11)

<< Chapter < Page
  Ut austin - principles of     Page 6 / 11
Chapter >> Page >

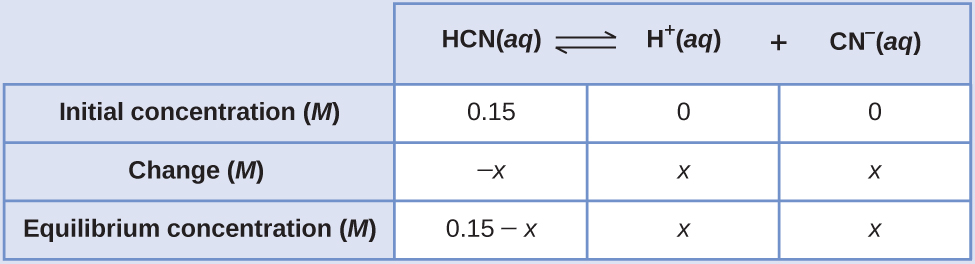
Recall that a small K c means that very little of the reactants form products and a large K c means that most of the reactants form products. If the system can be arranged so it starts “close” to equilibrium, then if the change ( x ) is small compared to any initial concentrations, it can be neglected. Small is usually defined as resulting in an error of less than 5%. The following two examples demonstrate this.

Approximate solution starting close to equilibrium

What are the concentrations at equilibrium of a 0.15 M solution of HCN?

HCN ( a q ) ⇌ H + ( a q ) + CN − ( a q ) K c = 4.9 × 10 −10

Solution

Using “ x ” to represent the concentration of each product at equilibrium gives this ICE table.

This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following: Initial pressure ( M ), Change ( M ), Equilibrium ( M ). The second column has the header, “H C N ( a q ) equilibrium arrow H superscript plus sign ( a q ) plus C N subscript negative sign ( a q ).” Under the second column is a subgroup of three columns and three rows. The first column has the following: 0.15, negative x, 0.15 minus x. The second column has the following: 0, x, x. The third column has the following: 0, x, x.

The exact solution may be obtained using the quadratic formula with

K c = ( x ) ( x ) 0.15 − x

solving

x 2 + 4.9 × 10 −10 − 7.35 × 10 −11 = 0
x = 8.56 × 10 −6 M ( 3 sig. figs. ) = 8.6 × 10 −6 M ( 2 sig. figs. )

Thus [H + ] = [CN – ] = x = 8.6 × 10 –6 M and [HCN] = 0.15 – x = 0.15 M .

In this case, chemical intuition can provide a simpler solution. From the equilibrium constant and the initial conditions, x must be small compared to 0.15 M . More formally, if x ≪ 0.15 , then 0.15 – x ≈ 0.15. If this assumption is true, then it simplifies obtaining x

K c = ( x ) ( x ) 0.15 − x ≈ x 2 0.15
4.9 × 10 −10 = x 2 0.15
x 2 = ( 0.15 ) ( 4.9 × 10 −10 ) = 7.4 × 10 −11
x = 7.4 × 10 −11 = 8.6 × 10 −6 M

In this example, solving the exact (quadratic) equation and using approximations gave the same result to two significant figures. While most of the time the approximation is a bit different from the exact solution, as long as the error is less than 5%, the approximate solution is considered valid. In this problem, the 5% applies to IF (0.15 – x ) ≈ 0.15 M , so if

x 0.15 × 100 % = 8.6 × 10 −6 0.15 × 100 % = 0.006 %

is less than 5%, as it is in this case, the assumption is valid. The approximate solution is thus a valid solution.

Check your learning

What are the equilibrium concentrations in a 0.25 M NH 3 solution?

NH 3 ( a q ) + H 2 O ( l ) ⇌ NH 4 + ( a q ) + OH − ( a q ) K c = 1.8 × 10 −5

Assume that x is much less than 0.25 M and calculate the error in your assumption.

Answer:

[ OH − ] = [ NH 4 + ] = 0.0021 M ; [NH 3 ] = 0.25 M , error = 0.84%

Got questions? Get instant answers now!

The second example requires that the original information be processed a bit, but it still can be solved using a small x approximation.

Approximate solution after shifting starting concentration

Copper(II) ions form a complex ion in the presence of ammonia

Cu 2+ ( a q ) + 4NH 3 ( a q ) ⇌ Cu ( NH 3 ) 4 2+ ( a q ) K c = 5.0 × 10 13 = [ Cu ( NH 3 ) 4 2+ ] [ Cu 2+ ( a q ) ] [ NH 3 ] 4

If 0.010 mol Cu 2+ is added to 1.00 L of a solution that is 1.00 M NH 3 what are the concentrations when the system comes to equilibrium?

Solution

The initial concentration of copper(II) is 0.010 M . The equilibrium constant is very large so it would be better to start with as much product as possible because “all products” is much closer to equilibrium than “all reactants.” Note that Cu 2+ is the limiting reactant; if all 0.010 M of it reacts to form product the concentrations would be

[ Cu 2+ ] = 0.010 − 0.010 = 0 M
[ Cu ( NH 3 ) 4 2+ ] = 0.010 M
[ NH 3 ] = 1.00 − 4 × 0.010 = 0.96 M

Using these “shifted” values as initial concentrations with x as the free copper(II) ion concentration at equilibrium gives this ICE table.

This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following: Initial pressure ( M ), Change ( M ), Equilibrium ( M ). The second column has the header, “C u superscript 2 positive sign ( a q ) plus 4 N H subscript 3 ( a q ) equilibrium arrow C u ( N H subscript 3 ) subscript 4 superscript 2 positive sign ( a q ).” Under the second column is a subgroup of three columns and three rows. The first column has the following: 0, positive x, x. The second column has the following: 0.96, positive 4 x, 0.96 plus 4 x. The third column has the following: 0.010, negative x, 0.010 minus x.

Since we are starting close to equilibrium, x should be small so that

0.96 + 4 x ≈ 0.96 M
0.010 − x ≈ 0.010 M
K c = ( 0.010 − x ) x ( 0.96 − 4 x ) 4 ≈ ( 0.010 ) x ( 0.96 ) 4 = 5.0 × 10 13
x = ( 0.010 ) K c ( 0.96 ) 4 = 2.4 × 10 −16 M

Select the smallest concentration for the 5% rule.

2.4 × 10 −16 0.010 × 100 % = 2 × 10 −12 %

This is much less than 5%, so the assumptions are valid. The concentrations at equilibrium are

[ Cu 2+ ] = x = 2.4 × 10 −16 M
[ NH 3 ] = 0.96 − 4 x = 0.96 M
[ Cu ( NH 3 ) 4 2+ ] = 0.010 − x = 0.010 M

By starting with the maximum amount of product, this system was near equilibrium and the change ( x ) was very small. With only a small change required to get to equilibrium, the equation for x was greatly simplified and gave a valid result well within the 5% error maximum.

Check your learning

What are the equilibrium concentrations when 0.25 mol Ni 2+ is added to 1.00 L of 2.00 M NH 3 solution?

Ni 2+ ( a q ) + 6NH 3 ( a q ) ⇌ Ni ( NH 3 ) 6 2+ ( a q ) K c = 5.5 × 10 8

With such a large equilibrium constant, first form as much product as possible, then assume that only a small amount ( x ) of the product shifts left. Calculate the error in your assumption.

Answer:

[ Ni ( NH 3 ) 6 2+ ] = 0.25 M , [NH 3 ] = 0.50 M , [Ni 2+ ] = 2.9 × 10 –8 M , error = 1.2 × 10 –5 %

Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Ut austin - principles of chemistry. OpenStax CNX. Mar 31, 2016 Download for free at http://legacy.cnx.org/content/col11830/1.13
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Ut austin - principles of chemistry' conversation and receive update notifications?

Ask