7.2 The second condition for equilibrium  (Page 2/8)

so that

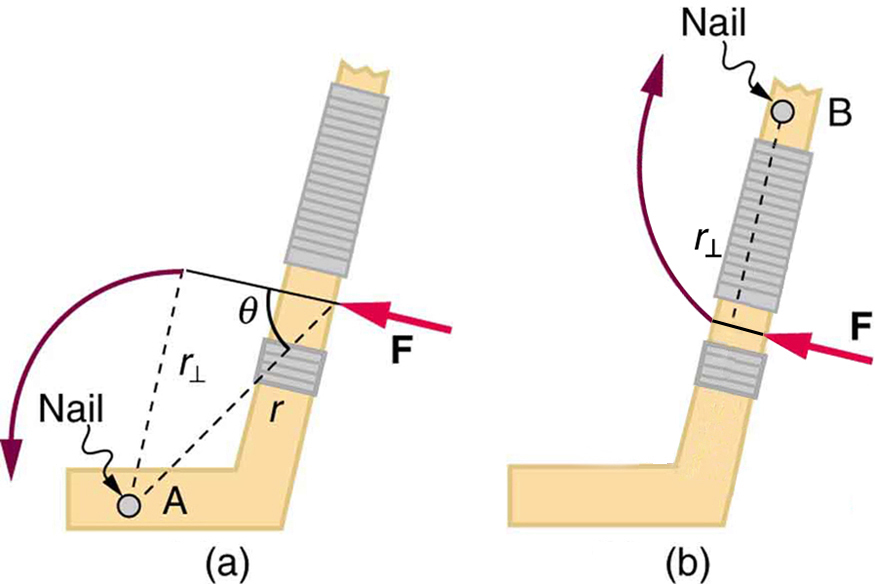
The perpendicular lever arm $r_{\perp }$ is the shortest distance from the pivot point to the line along which $\mathbf{\text{F}}$ acts; it is shown as a dashed line in [link] and [link] . Note that the line segment that defines the distance $r_{\perp }$ is perpendicular to $\mathbf{\text{F}}$ , as its name implies. It is sometimes easier to find or visualize $r_{\perp }$ than to find both $r$ and $\theta$ . In such cases, it may be more convenient to use $\tau =r_{\perp }F$ rather than $\tau =\text{rF}\text{sin}\theta$ for torque, but both are equally valid.

The SI unit of torque is newtons times meters, usually written as $\text{N}·\text{m}$ . For example, if you push perpendicular to the door with a force of 40 N at a distance of 0.800 m from the hinges, you exert a torque of $\text{32 N·m(0.800 m×40 N×sin 90º)}$ relative to the hinges. If you reduce the force to 20 N, the torque is reduced to $\text{16 N·m}$ , and so on.

The torque is always calculated with reference to some chosen pivot point. For the same applied force, a different choice for the location of the pivot will give you a different value for the torque, since both $r$ and $\theta$ depend on the location of the pivot. Any point in any object can be chosen to calculate the torque about that point. The object may not actually pivot about the chosen “pivot point.”

Note that for rotation in a plane, torque has two possible directions. Torque is either clockwise or counterclockwise relative to the chosen pivot point, as illustrated for points B and A, respectively, in [link] . If the object can rotate about point A, it will rotate counterclockwise, which means that the torque for the force is shown as counterclockwise relative to A. But if the object can rotate about point B, it will rotate clockwise, which means the torque for the force shown is clockwise relative to B. Also, the magnitude of the torque is greater when the lever arm is longer.

Now, the second condition necessary to achieve equilibrium is that the net external torque on a system must be zero . An external torque is one that is created by an external force. You can choose the point around which the torque is calculated. The point can be the physical pivot point of a system or any other point in space—but it must be the same point for all torques. If the second condition (net external torque on a system is zero) is satisfied for one choice of pivot point, it will also hold true for any other choice of pivot point in or out of the system of interest. (This is true only in an inertial frame of reference.) The second condition necessary to achieve equilibrium is stated in equation form as