| << Chapter < Page | Chapter >> Page > |
Identify each of the following as rational or irrational:
ⓐ ⓑ ⓒ
Identify each of the following as rational or irrational:
ⓐ ⓑ ⓒ
Let's think about square roots now. Square roots of perfect squares are always whole numbers , so they are rational. But the decimal forms of square roots of numbers that are not perfect squares never stop and never repeat, so these square roots are irrational.
Identify each of the following as rational or irrational:
ⓐ
ⓑ
ⓐ The number is a perfect square, since So Therefore is rational.
ⓑ Remember that and so is not a perfect square.
This means is irrational.
Identify each of the following as rational or irrational:
ⓐ
ⓑ
Identify each of the following as rational or irrational:
ⓐ
ⓑ
We have seen that all counting numbers are whole numbers, all whole numbers are integers, and all integers are rational numbers . Irrational numbers are a separate category of their own. When we put together the rational numbers and the irrational numbers , we get the set of real numbers .
[link] illustrates how the number sets are related.
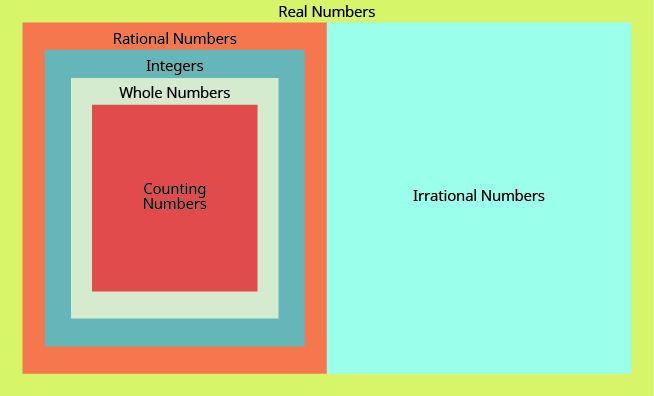
Real numbers are numbers that are either rational or irrational.
Does the term “real numbers” seem strange to you? Are there any numbers that are not “real”, and, if so, what could they be? For centuries, the only numbers people knew about were what we now call the real numbers. Then mathematicians discovered the set of imaginary numbers. You won't encounter imaginary numbers in this course, but you will later on in your studies of algebra.
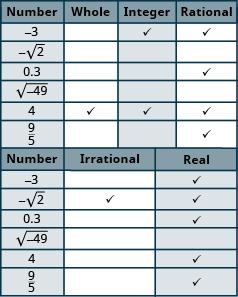
Determine whether each of the numbers in the following list is a ⓐ whole number, ⓑ integer, ⓒ rational number, ⓓ irrational number, and ⓔ real number.
ⓐ The whole numbers are The number is the only whole number given.
ⓑ The integers are the whole numbers, their opposites, and From the given numbers, and are integers. Also, notice that is the square of so So the integers are
ⓒ Since all integers are rational, the numbers are also rational. Rational numbers also include fractions and decimals that terminate or repeat, so are rational.
ⓓ The number is not a perfect square, so is irrational.
ⓔ All of the numbers listed are real.
We'll summarize the results in a table.
| Number | Whole | Integer | Rational | Irrational | Real |
|---|---|---|---|---|---|
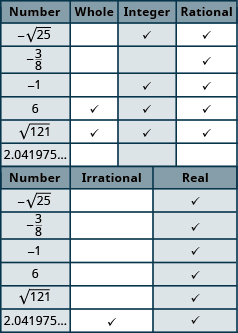
Determine whether each number is a ⓐ whole number, ⓑ integer, ⓒ rational number, ⓓ irrational number, and ⓔ real number:
Determine whether each number is a ⓐ whole number, ⓑ integer, ⓒ rational number, ⓓ irrational number, and ⓔ real number:

Rational Numbers
In the following exercises, write as the ratio of two integers.
In the following exercises, determine which of the given numbers are rational and which are irrational.
In the following exercises, identify whether each number is rational or irrational.
Classifying Real Numbers
In the following exercises, determine whether each number is whole, integer, rational, irrational, and real.
, , , , ,
Field trip All the graders at Lincoln Elementary School will go on a field trip to the science museum. Counting all the children, teachers, and chaperones, there will be people. Each bus holds people.
ⓐ How many buses will be needed?
ⓑ Why must the answer be a whole number?
ⓒ Why shouldn't you round the answer the usual way?
Child care Serena wants to open a licensed child care center. Her state requires that there be no more than children for each teacher. She would like her child care center to serve children.
ⓐ How many teachers will be needed?
ⓑ Why must the answer be a whole number?
ⓒ Why shouldn't you round the answer the usual way?
In your own words, explain the difference between a rational number and an irrational number.
Explain how the sets of numbers (counting, whole, integer, rational, irrationals, reals) are related to each other.
Answers will vary.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?