| << Chapter < Page | Chapter >> Page > |
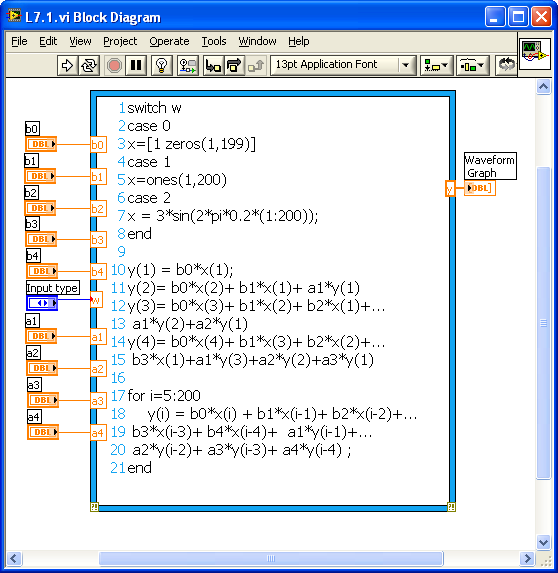
This lab involves analyzing the response of discrete-time systems. Responses are calculated for three different kinds of inputs; impulse, step and sine. [link] shows the completed block diagram. Connect the input variable w to an Enum Control so that an input type (impulse, step or sine) can be selected. The response of this system to any discrete-time input can be written as
For this example, consider five b’s and four a’s. The system output is displayed using a waveform graph.
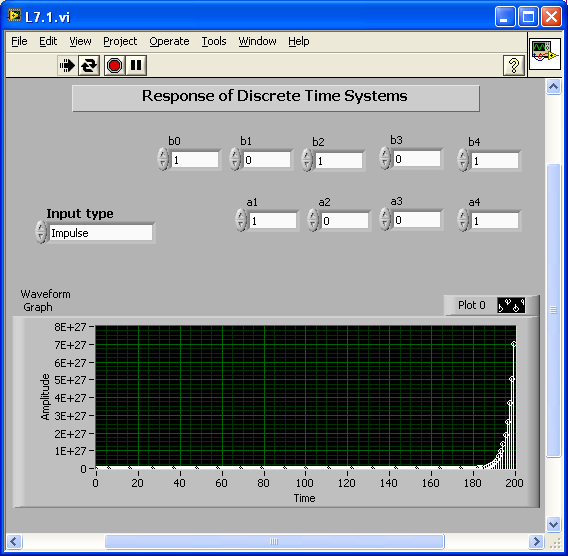
[link] shows the front panel of the above system. The front panel can be used to interactively select the input type and set the coefficients a and b. The system response for a particular type of input (impulse, step or sine) is shown in the waveform graph.
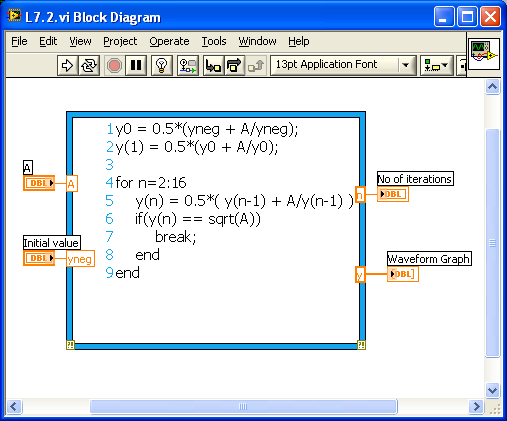
As another example of discrete-time systems, let us consider taking the square root of an integer number. Often computers and calculators compute the square root of a positive number using the following recursive equation:
If the input to this equation is set as a step function of amplitude A, then converges to the square root of A after several iterations.
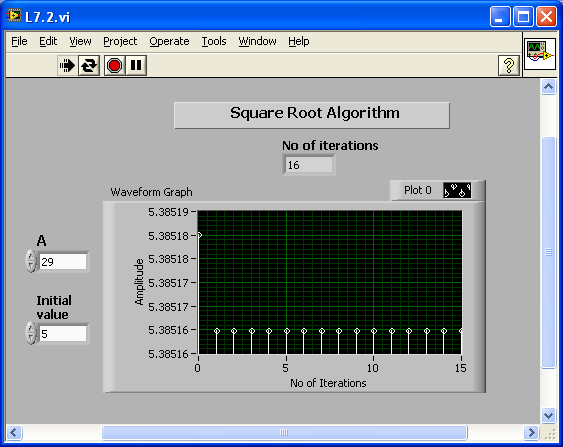
[link] shows the block diagram for a square root computation system. The number of iterations required to converge to the true value is shown in the output. The initial condition Initial value is set as a control. [link] shows the corresponding front panel.
In this section, let us examine a basic analog and digital filtering example by implementing a lowpass and a highpass filter in the analog and digital domains, respectively. [link] shows the completed block diagram of the filtering system. For analog approximation of the signals, use a higher sampling rate (dw1=0.01). To detect whether the filtering is lowpass or highpass, use the Enum Control Analog filter type. Calculate the magnitude and phase response of these filters using equations provided in Chapter 7 for analog and digital filters. Set the values of R and C as controls, and display the responses using a Build Waveform function and a waveform graph.
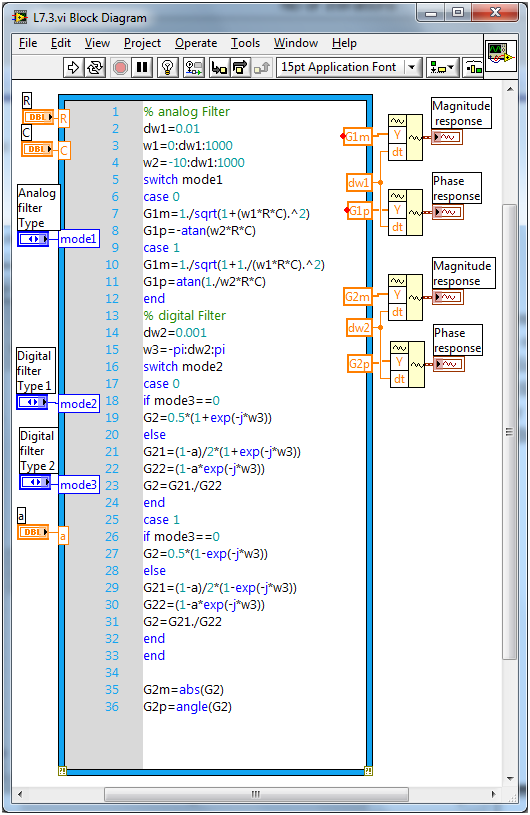
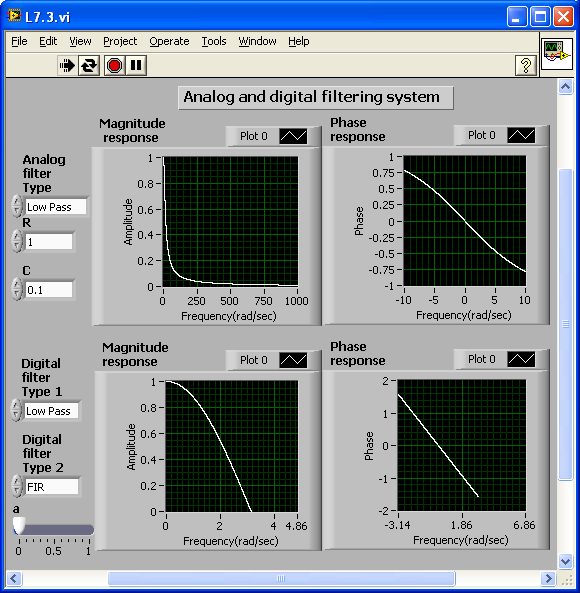
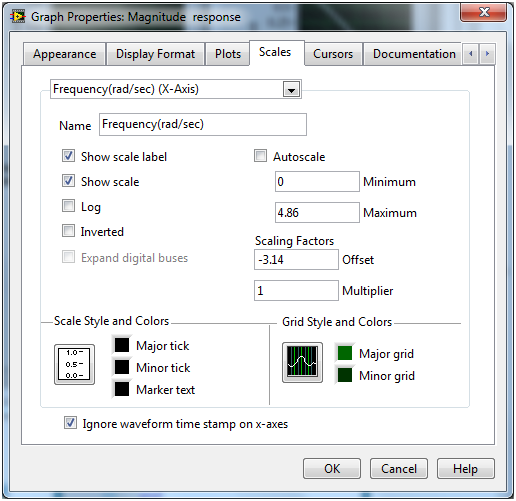
For the digital case, use a lower sampling rate (dw2=0.001). With the Enum controls Digital filter type 1 and Digital filter type 2, select lowpass or highpass and FIR or IIR filter type. Use a Build Waveform function and a waveform graph to display the magnitude and phase responses of the digital filters. [link] shows the front panel of this filtering system. For a better view of magnitude response of the digital filter, set the properties of the waveform graph as shown in [link] .
Bandpass and Bandstop Filters
Use the lowpass and highpass filters (both analog and digital) described in Analog and Digital Filtering section to construct bandpass and bandstop filters. The bandpass filter should be able to pass signals from 50 to 200 Hz and the bandstop filter should be able to stop signals from 150 to 400 Hz. Determine the values of R and C required for this analog filter design. Also, determine the values of the coefficients required for an equivalent IIR digital filter design.
Insert Solution Text Here
Noise Reduction
Use an analog lowpass filter to remove the high-frequency noise described in Noise Reduction example of Lab 5. Repeat using a digital lowpass filter.
Insert Solution Text Here
Frequency Division Multiplexing (FDM)
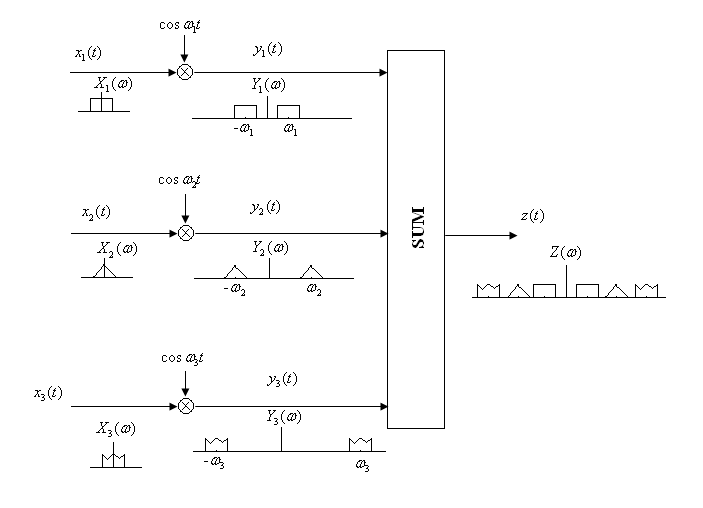
FDM is widely used in digital communication to simultaneously transmit multiple signals over a single wideband channel (for details, refer to
[link] ). For FDM communication, individual signals are multiplied with different carriers to avoid overlaps in the frequency domain. Their time domain processing and corresponding frequency spectrums are shown in
[link] . Build a VI to implement an FDM communication system for three signals
and
. Use the files
Insert Solution Text Here
FDM Detector
Build a VI to implement an FDM detector system for detecting the signal as shown in [link] .
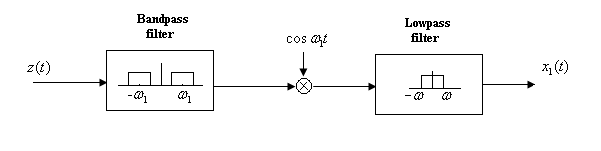
Insert Solution Text Here

Notification Switch
Would you like to follow the 'An interactive approach to signals and systems laboratory' conversation and receive update notifications?