7.1 Discrete time fourier series (dtfs)  (Page 5/2)

Introduction

In this module, we will derive an expansion for discrete-time, periodic functions, and in doing so, derive the Discrete Time Fourier Series (DTFS), or the Discrete Fourier Transform (DFT).

Dtfs

Eigenfunction analysis

Since complex exponentials are eigenfunctions of linear time-invariant (LTI) systems , calculating the output of an LTI system $\mathscr{H}$ given $e^{i\omega n}$ as an input amounts to simple multiplication, where ${\omega }_0=\frac{2\pi k}{N}$ , and where $H(k)\in \mathbb{C}$ is the eigenvalue corresponding to k. As shown in the figure, a simple exponential input would yield the output

Using this and the fact that $\mathscr{H}$ is linear, calculating $y(n)$ for combinations of complex exponentials is also straightforward.

$$c_{1}e^{i{\omega }_{1}n}+c_{2}e^{i{\omega }_{2}n}\to c_{1}H(k_1)e^{i{\omega }_{1}n}+c_{2}H(k_2)e^{i{\omega }_{1}n}$$ $$\sum c_{l}e^{i{\omega }_{\mathrm{l}}n}\to \sum c_{l}H(k_l)e^{i{\omega }_{\mathrm{l}}n}$$

The action of $H$ on an input such as those in the two equations above is easy to explain. $\mathscr{H}$ independently scales each exponential component $e^{i{\omega }_{\mathrm{l}}n}$ by a different complex number $H(k_l)\in \mathbb{C}$ . As such, if we can write a function $y(n)$ as a combination of complex exponentials it allows us to easily calculate the output of a system.

Dtfs synthesis

It can be demonstrated that an arbitrary Discrete Time-periodic function $f(n)$ can be written as a linear combination of harmonic complex sinusoids

The $c_n$ - called the Fourier coefficients - tell us "how much" of the sinusoid $e^{j{\omega }_{0}kn}$ is in $f(n)$ . The formula shows $f(n)$ as a sum of complex exponentials, each of which is easily processed by an LTI system (since it is an eigenfunction of every LTI system). Mathematically, it tells us that the set ofcomplex exponentials $\{\forall k, k\in \mathbb{Z}\colon e^{j{\omega }_{0}kn}\}$ form a basis for the space of N-periodic discrete time functions.

Dft synthesis demonstration

Dtfs analysis

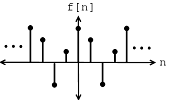
Say we have the following set of numbers that describe a periodic,discrete-time signal, where $N=4$ : $$\{\dots , 3, 2, -2, 1, 3, \dots \}$$ Such a periodic, discrete-time signal (with period $N$ ) can be thought of as a finite set of numbers. For example, we can represent this signal as either a periodic signal or asjust a single interval as follows: