6.8 Torque on a current loop: motors and meters  (Page 8/4)

Motors are the most common application of magnetic force on current-carrying wires. Motors have loops of wire in a magnetic field. When current is passed through the loops, the magnetic field exerts torque on the loops, which rotates a shaft. Electrical energy is converted to mechanical work in the process. (See [link] .)

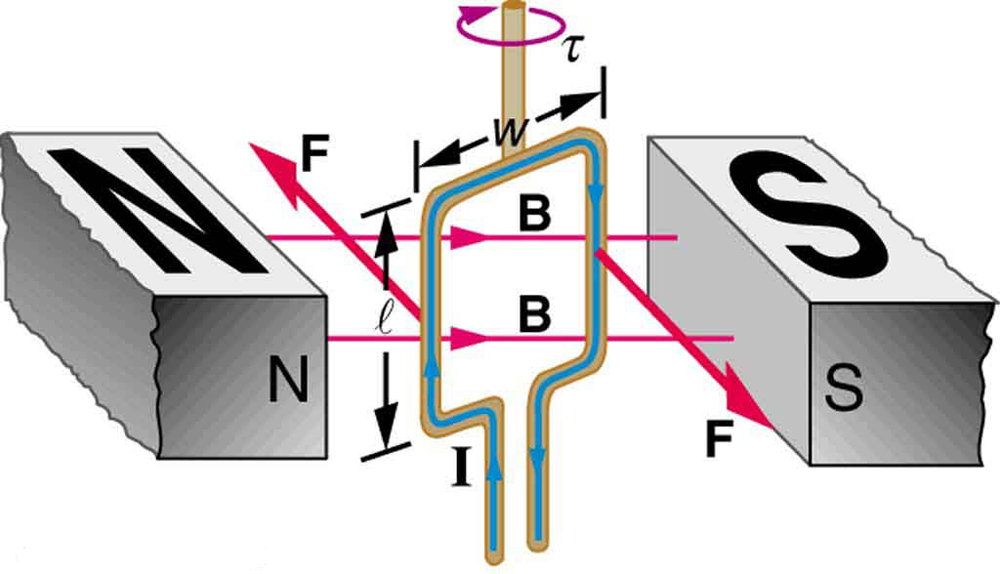
Let us examine the force on each segment of the loop in [link] to find the torques produced about the axis of the vertical shaft. (This will lead to a useful equation for the torque on the loop.) We take the magnetic field to be uniform over the rectangular loop, which has width $w$ and height $l$ . First, we note that the forces on the top and bottom segments are vertical and, therefore, parallel to the shaft, producing no torque. Those vertical forces are equal in magnitude and opposite in direction, so that they also produce no net force on the loop. [link] shows views of the loop from above. Torque is defined as $\tau =\text{rF}\text{sin}\theta$ , where $F$ is the force, $r$ is the distance from the pivot that the force is applied, and $\theta$ is the angle between $r$ and $F$ . As seen in [link] (a), right hand rule 1 gives the forces on the sides to be equal in magnitude and opposite in direction, so that the net force is again zero. However, each force produces a clockwise torque. Since $r=w/2$ , the torque on each vertical segment is $(w/2)F\text{sin}\theta$ , and the two add to give a total torque.

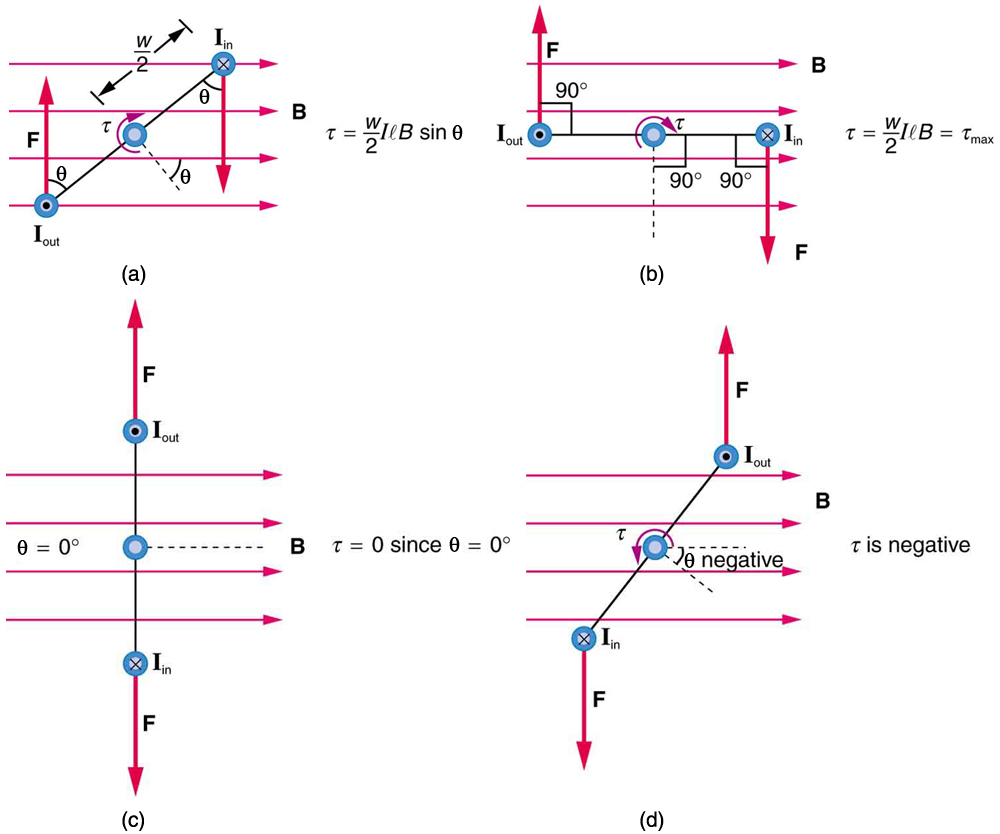
Now, each vertical segment has a length $l$ that is perpendicular to $B$ , so that the force on each is $F=\text{IlB}$ . Entering $F$ into the expression for torque yields

If we have a multiple loop of $N$ turns, we get $N$ times the torque of one loop. Finally, note that the area of the loop is $A=\text{wl}$ ; the expression for the torque becomes

This is the torque on a current-carrying loop in a uniform magnetic field. This equation can be shown to be valid for a loop of any shape. The loop carries a current $I$ , has $N$ turns, each of area $A$ , and the perpendicular to the loop makes an angle $\theta$ with the field $B$ . The net force on the loop is zero.