1. Home
  2. Engr 2113 ece math
  3. Continuous random variables
  4. Review

6.8 Review

<< Chapter < Page
  Engr 2113 ece math   Page 1 / 1
Chapter >> Page >
This module provides a number of homework/review problems related to Continuous Random Variables.

[link] – [link] refer to the following study: A recent study of mothers of junior high school children in Santa Clara County reported that 76% of the mothers are employed in paid positions. Of those mothers who are employed, 64% work full-time (over 35 hours per week), and 36% work part-time. However, out of all of the mothers in the population, 49% work full-time. The population under study is made up of mothers of junior high school children in Santa Clara County.

Let E = size 12{E={}} {} employed, Let F = size 12{F={}} {} full-time employment

  • Find the percent of all mothers in the population that NOT employed.
  • Find the percent of mothers in the population that are employed part-time.
  • 24%
  • 27%

The type of employment is considered to be what type of data?

Qualitative

Find the probability that a randomly selected mother works part-time given that she is employed.

0.36

Find the probability that a randomly selected person from the population will be employed OR work full-time.

0.7636

Based upon the above information, are being employed AND working part-time:

  • mutually exclusive events? Why or why not?
  • independent events? Why or why not?
  • No,
  • No,

[link] - [link] refer to the following: We randomly pick 10 mothers from the above population. We are interested in the number of the mothers that are employed. Let X = size 12{X={}} {} number of mothers that are employed.

State the distribution for X size 12{X} {} .

B ( 10 , 0 . 76 ) size 12{B \( "10",0 "." "76" \) } {}

Find the probability that at least 6 are employed.

0.9330

We expect the Statistics Discussion Board to have, on average, 14 questions posted to it per week. We are interested in the number of questions posted to it per day.

  • Define X size 12{X} {} .
  • What are the values that the random variable may take on?
  • State the distribution for X size 12{X} {} .
  • Find the probability that from 10 to 14 (inclusive) questions are posted to the Listserv on a randomly picked day.
  • X = size 12{X={}} {} the number of questions posted to the Statistics Listserv per day
  • x = 0,1,2, . . . size 12{x=0,1,2, "." "." "." } {}
  • X ~ P ( 2 ) size 12{X "~" P \( 2 \) } {}
  • 0

A person invests $1000 in stock of a company that hopes to go public in 1 year.

  • The probability that the person will lose all his money after 1 year (i.e. his stock will be worthless) is 35%.
  • The probability that the person’s stock will still have a value of $1000 after 1 year (i.e. no profit and no loss) is 60%.
  • The probability that the person’s stock will increase in value by $10,000 after 1 year (i.e. will be worth $11,000) is 5%.

Find the expected PROFIT after 1 year.

$150

Rachel’s piano cost $3000. The average cost for a piano is $4000 with a standard deviation of $2500. Becca’s guitar cost $550. The average cost for a guitar is $500 with a standard deviation of $200.Matt’s drums cost $600. The average cost for drums is $700 with a standard deviation of $100. Whose cost was lowest when compared to his or her own instrument? Justify your answer.

Matt

Horizontal boxplot with first whisker extending from 1 to 2, box from 2 to 5, line at 4, and second whisker extending from 5 to 7.

For each statement below, explain why each is either true or false.

  • 25% of the data are at most 5.
  • There is the same amount of data from 4 – 5 as there is from 5 – 7.
  • There are no data values of 3.
  • 50% of the data are 4.
  • False
  • True
  • False
  • False

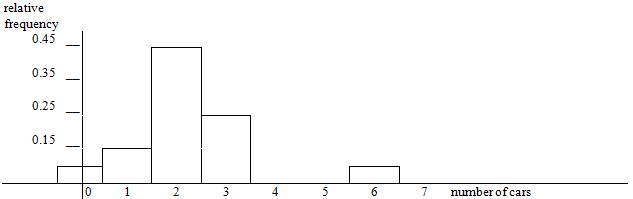
[link] – [link] refer to the following: 64 faculty members were asked the number of cars they owned (including spouse and children’s cars). The results are given in the following graph: Histogram consisting of 5 bars with number of cars, from 0-7 in increments of 1, on the x-axis, and frequency, in increments of 0.1 from 0.15-0.45, on the y-axis. No bars exist for 4, 5, or 7. Bar 0 has a frequency of 0.075, 1 has 0.15, 2 has 0.45, 3 has 0.25, and 6 has 0.075.

Find the approximate number of responses that were “3.”

16

Find the first, second and third quartiles. Use them to construct a box plot of the data.

2,2,3 size 12{2,2,3} {}

[link] – [link] refer to the following study done of the Girls soccer team “Snow Leopards”:

Hair Style Hair Color
blond brown black
ponytail 3 2 5
plain 2 2 1
Suppose that one girl from the Snow Leopards is randomly selected.

Find the probability that the girl has black hair GIVEN that she wears a ponytail.

5 10 = 0 . 5 size 12{ { {5} over {"10"} } =0 "." 5} {}

Find the probability that the girl wears her hair plain OR has brown hair.

7 15 size 12{ { {7} over {"15"} } } {}

Find the probability that the girl has blond hair AND that she wears her hair plain.

2 15 size 12{ { {2} over {"15"} } } {}

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Engr 2113 ece math. OpenStax CNX. Aug 27, 2010 Download for free at http://cnx.org/content/col11224/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Engr 2113 ece math' conversation and receive update notifications?

Ask