| << Chapter < Page | Chapter >> Page > |
In this section, we study Stokes’ theorem, a higher-dimensional generalization of Green’s theorem. This theorem, like the Fundamental Theorem for Line Integrals and Green’s theorem, is a generalization of the Fundamental Theorem of Calculus to higher dimensions. Stokes’ theorem relates a vector surface integral over surface S in space to a line integral around the boundary of S . Therefore, just as the theorems before it, Stokes’ theorem can be used to reduce an integral over a geometric object S to an integral over the boundary of S .
In addition to allowing us to translate between line integrals and surface integrals, Stokes’ theorem connects the concepts of curl and circulation. Furthermore, the theorem has applications in fluid mechanics and electromagnetism. We use Stokes’ theorem to derive Faraday’s law, an important result involving electric fields.
Stokes’ theorem says we can calculate the flux of curl F across surface S by knowing information only about the values of F along the boundary of S . Conversely, we can calculate the line integral of vector field F along the boundary of surface S by translating to a double integral of the curl of F over S .
Let S be an oriented smooth surface with unit normal vector N . Furthermore, suppose the boundary of S is a simple closed curve C . The orientation of S induces the positive orientation of C if, as you walk in the positive direction around C with your head pointing in the direction of N , the surface is always on your left. With this definition in place, we can state Stokes’ theorem.
Let S be a piecewise smooth oriented surface with a boundary that is a simple closed curve C with positive orientation ( [link] ). If F is a vector field with component functions that have continuous partial derivatives on an open region containing S , then
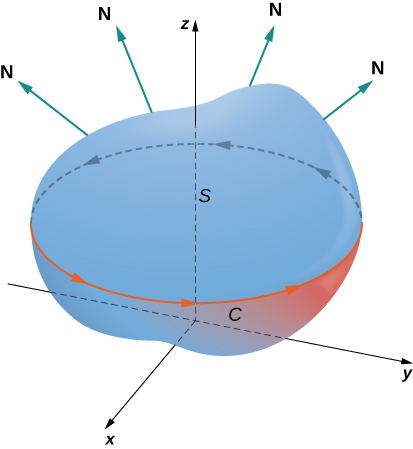
Suppose surface S is a flat region in the xy -plane with upward orientation. Then the unit normal vector is k and surface integral is actually the double integral In this special case, Stokes’ theorem gives However, this is the flux form of Green’s theorem, which shows us that Green’s theorem is a special case of Stokes’ theorem. Green’s theorem can only handle surfaces in a plane, but Stokes’ theorem can handle surfaces in a plane or in space.
The complete proof of Stokes’ theorem is beyond the scope of this text. We look at an intuitive explanation for the truth of the theorem and then see proof of the theorem in the special case that surface S is a portion of a graph of a function, and S , the boundary of S, and F are all fairly tame.
First, we look at an informal proof of the theorem. This proof is not rigorous, but it is meant to give a general feeling for why the theorem is true. Let S be a surface and let D be a small piece of the surface so that D does not share any points with the boundary of S . We choose D to be small enough so that it can be approximated by an oriented square E . Let D inherit its orientation from S , and give E the same orientation. This square has four sides; denote them and for the left, right, up, and down sides, respectively. On the square, we can use the flux form of Green’s theorem:

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?