6.5 Force on a moving charge in a magnetic field: examples and  (Page 5/4)

Magnetic force can cause a charged particle to move in a circular or spiral path. Cosmic rays are energetic charged particles in outer space, some of which approach the Earth. They can be forced into spiral paths by the Earth’s magnetic field. Protons in giant accelerators are kept in a circular path by magnetic force. The bubble chamber photograph in [link] shows charged particles moving in such curved paths. The curved paths of charged particles in magnetic fields are the basis of a number of phenomena and can even be used analytically, such as in a mass spectrometer.

So does the magnetic force cause circular motion? Magnetic force is always perpendicular to velocity, so that it does no work on the charged particle. The particle’s kinetic energy and speed thus remain constant. The direction of motion is affected, but not the speed. This is typical of uniform circular motion. The simplest case occurs when a charged particle moves perpendicular to a uniform $B$ -field, such as shown in [link] . (If this takes place in a vacuum, the magnetic field is the dominant factor determining the motion.) Here, the magnetic force supplies the centripetal force $F_{\mathrm{c}}={\text{mv}}^2/r$ . Noting that $\text{sin}\theta =1$ , we see that $F=\text{qvB}$ .

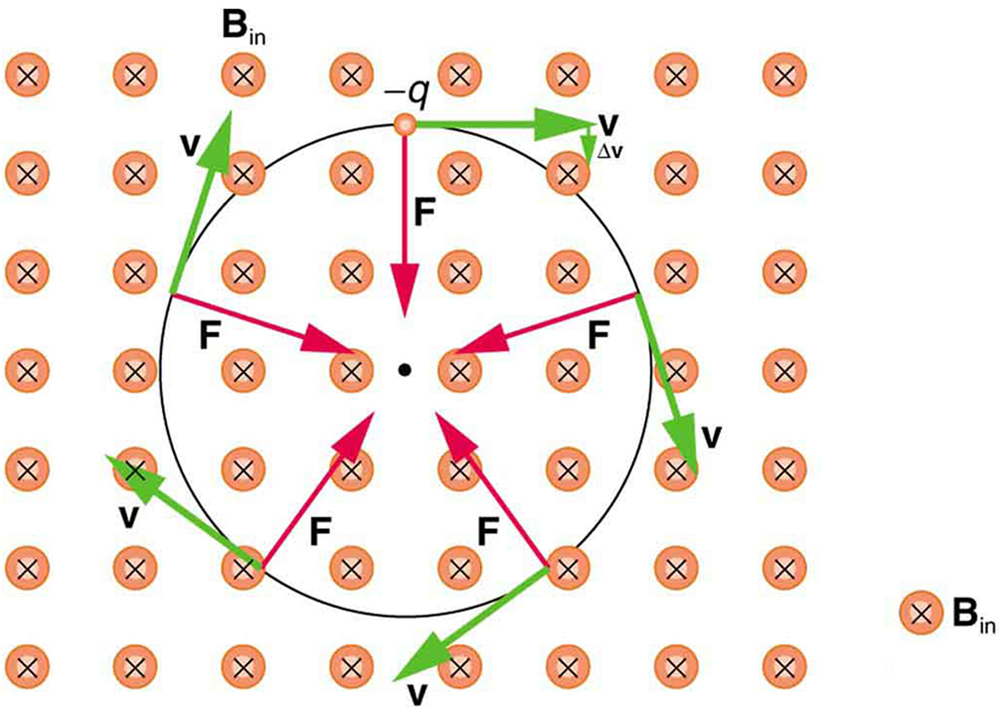
Because the magnetic force $F$ supplies the centripetal force $F_{\mathrm{c}}$ , we have

Solving for $r$ yields

Here, $r$ is the radius of curvature of the path of a charged particle with mass $m$ and charge $q$ , moving at a speed $v$ perpendicular to a magnetic field of strength $B$ . If the velocity is not perpendicular to the magnetic field, then $v$ is the component of the velocity perpendicular to the field. The component of the velocity parallel to the field is unaffected, since the magnetic force is zero for motion parallel to the field. This produces a spiral motion rather than a circular one.

Calculating the curvature of the path of an electron moving in a magnetic field: a magnet on a tv screen

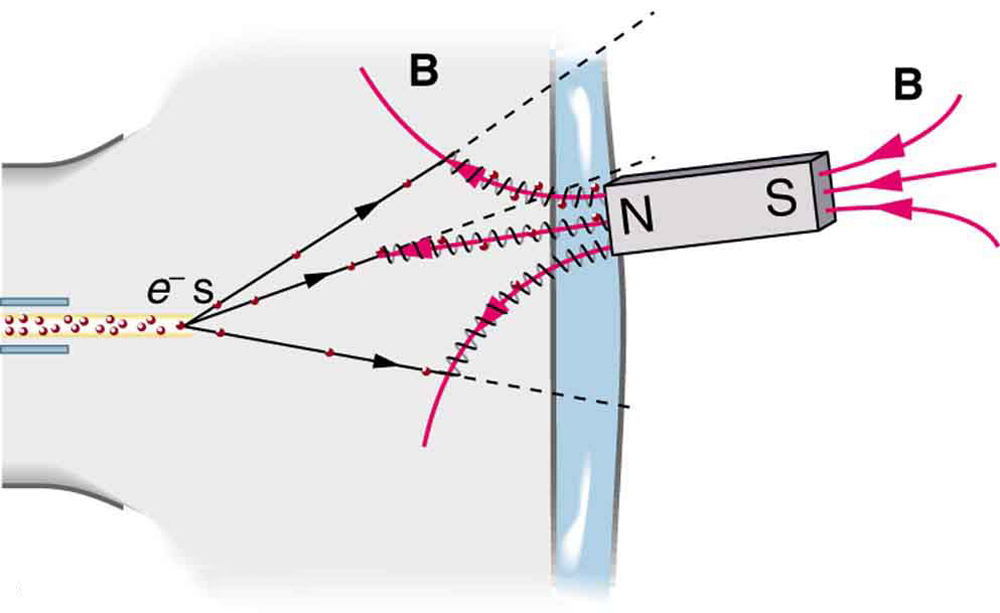
A magnet brought near an old-fashioned TV screen such as in [link] (TV sets with cathode ray tubes instead of LCD screens) severely distorts its picture by altering the path of the electrons that make its phosphors glow. (Don’t try this at home, as it will permanently magnetize and ruin the TV.) To illustrate this, calculate the radius of curvature of the path of an electron having a velocity of $6\text{.}\text{00}\times {\text{10}}^7\text{m/s}$ (corresponding to the accelerating voltage of about 10.0 kV used in some TVs) perpendicular to a magnetic field of strength $B=0\text{.500 T}$ (obtainable with permanent magnets).

Strategy

We can find the radius of curvature $r$ directly from the equation $r=\frac{mv}{qB}$ , since all other quantities in it are given or known.

Solution

Using known values for the mass and charge of an electron, along with the given values of $v$ and $B$ gives us

$\begin{array}{lll}r=\frac{\text{mv}}{\text{qB}}& =& \frac{\left(9\text{.}\text{11}\times {\text{10}}^{-\text{31}}\text{kg}\right)\left(6\text{.}\text{00}\times {\text{10}}^7\text{m/s}\right)}{\left(1\text{.}\text{60}\times {\text{10}}^{-\text{19}}\text{C}\right)\left(0\text{.}\text{500}\text{T}\right)}\\ & =& 6\text{.}\text{83}\times {\text{10}}^{-4}\text{m}\end{array}$

or

$r=0\text{.}\text{683 mm}.$

Discussion

The small radius indicates a large effect. The electrons in the TV picture tube are made to move in very tight circles, greatly altering their paths and distorting the image.