| << Chapter < Page | Chapter >> Page > |
Climbing stairs and lifting objects is work in both the scientific and everyday sense—it is work done against the gravitational force. When there is work, there is a transformation of energy. The work done against the gravitational force goes into an important form of stored energy that we will explore in this section.
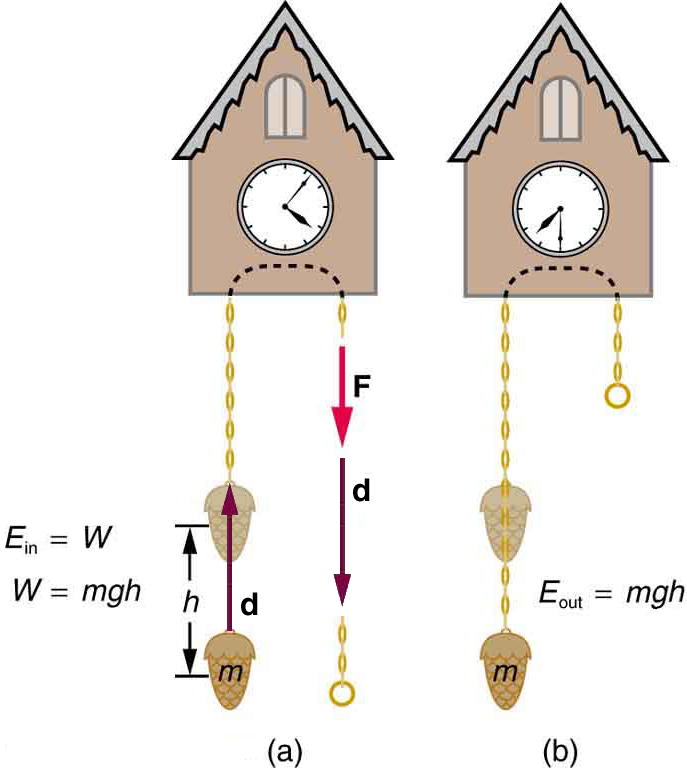
Let us calculate the work done in lifting an object of mass through a height , such as in [link] . If the object is lifted straight up at constant speed, then the force needed to lift it is equal to its weight . The work done on the mass is then . We define this to be the gravitational potential energy put into (or gained by) the object-Earth system. This energy is associated with the state of separation between two objects that attract each other by the gravitational force. For convenience, we refer to this as the gained by the object, recognizing that this is energy stored in the gravitational field of Earth. Why do we use the word “system”? Potential energy is a property of a system rather than of a single object—due to its physical position. An object’s gravitational potential is due to its position relative to the surroundings within the Earth-object system. The force applied to the object is an external force, from outside the system. When it does positive work it increases the gravitational potential energy of the system. Because gravitational potential energy depends on relative position, we need a reference level at which to set the potential energy equal to 0. We usually choose this point to be Earth’s surface, but this point is arbitrary; what is important is the difference in gravitational potential energy, because this difference is what relates to the work done. The difference in gravitational potential energy of an object (in the Earth-object system) between two rungs of a ladder will be the same for the first two rungs as for the last two rungs.
Gravitational potential energy may be converted to other forms of energy, such as kinetic energy. If we release the mass, gravitational force will do an amount of work equal to on it, thereby increasing its kinetic energy by that same amount (by the work-energy theorem). We will find it more useful to consider just the conversion of to without explicitly considering the intermediate step of work. (See [link] .) This shortcut makes it is easier to solve problems using energy (if possible) rather than explicitly using forces.

Notification Switch
Would you like to follow the 'Introduction to applied math and physics' conversation and receive update notifications?