6.3 Conservation of momentum  (Page 2/7)

where ${p\prime }_1$ and ${p\prime }_2$ are the momenta of cars 1 and 2 after the collision. (We often use primes to denote the final state.)

This result—that momentum is conserved—has validity far beyond the preceding one-dimensional case. It can be similarly shown that total momentum is conserved for any isolated system, with any number of objects in it. In equation form, the conservation of momentum principle    for an isolated system is written

or

where ${\mathbf{p}}_{\text{tot}}$ is the total momentum (the sum of the momenta of the individual objects in the system) and ${\mathbf{\text{p}}\prime }_{\text{tot}}$ is the total momentum some time later. (The total momentum can be shown to be the momentum of the center of mass of the system.) An isolated system    is defined to be one for which the net external force is zero $\left({\mathbf{\text{F}}}_{\text{net}}=0\right)\text{.}$

Perhaps an easier way to see that momentum is conserved for an isolated system is to consider Newton’s second law in terms of momentum, ${\mathbf{F}}_{\text{net}}=\frac{{\mathrm{\Delta }\mathbf{p}}_{\text{tot}}}{\mathrm{\Delta }t}$ . For an isolated system, $\left({\mathbf{\text{F}}}_{\text{net}}=0\right)$ ; thus, $\mathrm{\Delta }{\mathbf{p}}_{\text{tot}}=0$ , and ${\mathbf{p}}_{\text{tot}}$ is constant.

We have noted that the three length dimensions in nature— $x$ , $y$ , and $z$ —are independent, and it is interesting to note that momentum can be conserved in different ways along each dimension. For example, during projectile motion and where air resistance is negligible, momentum is conserved in the horizontal direction because horizontal forces are zero and momentum is unchanged. But along the vertical direction, the net vertical force is not zero and the momentum of the projectile is not conserved. (See [link] .) However, if the momentum of the projectile-Earth system is considered in the vertical direction, we find that the total momentum is conserved.

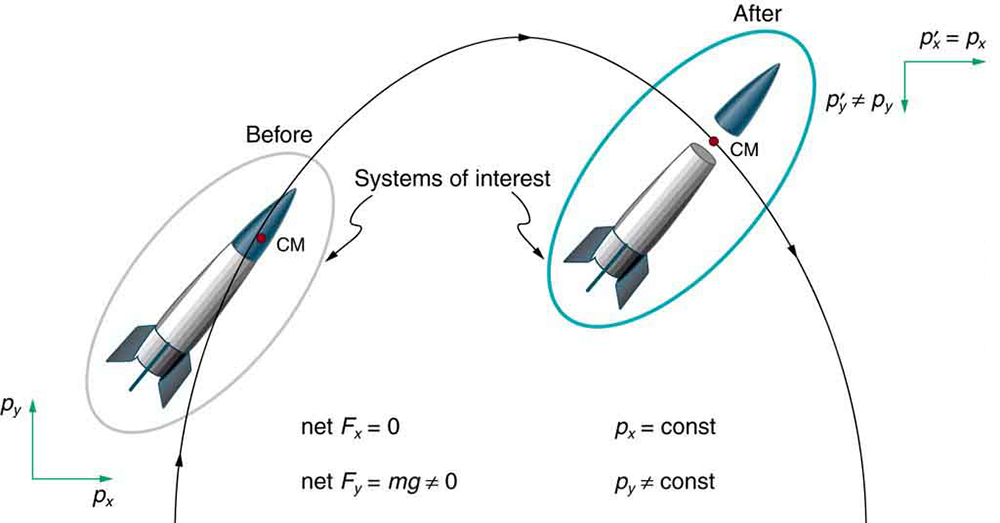
The conservation of momentum principle can be applied to systems as different as a comet striking Earth and a gas containing huge numbers of atoms and molecules. Conservation of momentum is violated only when the net external force is not zero. But another larger system can always be considered in which momentum is conserved by simply including the source of the external force. For example, in the collision of two cars considered above, the two-car system conserves momentum while each one-car system does not.