6.3 Applications of electrostatics  (Page 6/14)

Integrated Concepts

The practical limit to an electric field in air is about $3.00\times {10}^6\text{N/C}$ . Above this strength, sparking takes place because air begins to ionize and charges flow, reducing the field. (a) Calculate the distance a free proton must travel in this field to reach $\mathrm{3.00\%}$ of the speed of light, starting from rest. (b) Is this practical in air, or must it occur in a vacuum?

Integrated Concepts

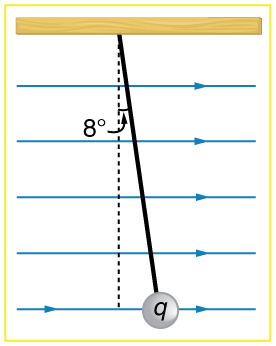
A 5.00 g charged insulating ball hangs on a 30.0 cm long string in a uniform horizontal electric field as shown in [link] . Given the charge on the ball is $1.00\mu \text{C}$ , find the strength of the field.

Integrated Concepts

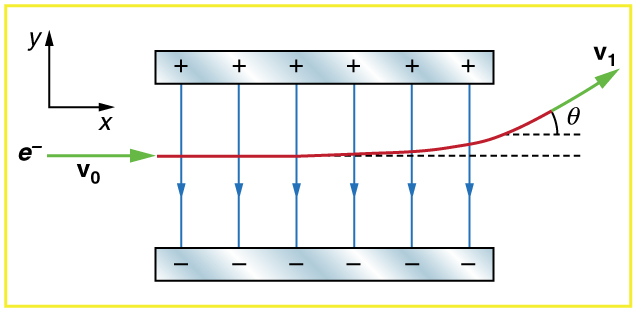
[link] shows an electron passing between two charged metal plates that create an 100 N/C vertical electric field perpendicular to the electron’s original horizontal velocity. (These can be used to change the electron’s direction, such as in an oscilloscope.) The initial speed of the electron is $3.00\times {10}^6\text{m/s}$ , and the horizontal distance it travels in the uniform field is 4.00 cm. (a) What is its vertical deflection? (b) What is the vertical component of its final velocity? (c) At what angle does it exit? Neglect any edge effects.

Integrated Concepts

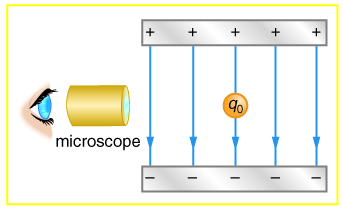
The classic Millikan oil drop experiment was the first to obtain an accurate measurement of the charge on an electron. In it, oil drops were suspended against the gravitational force by a vertical electric field. (See [link] .) Given the oil drop to be $1.00\mu \text{m}$ in radius and have a density of $\mathrm{920\; kg/}{\mathrm{m}}^3$ : (a) Find the weight of the drop. (b) If the drop has a single excess electron, find the electric field strength needed to balance its weight.

Integrated Concepts

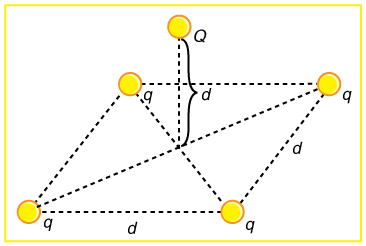
(a) In [link] , four equal charges $q$ lie on the corners of a square. A fifth charge $Q$ is on a mass $m$ directly above the center of the square, at a height equal to the length $d$ of one side of the square. Determine the magnitude of $q$ in terms of $Q$ , $m$ , and $d$ , if the Coulomb force is to equal the weight of $m$ . (b) Is this equilibrium stable or unstable? Discuss.

Unreasonable Results

(a) Calculate the electric field strength near a 10.0 cm diameter conducting sphere that has 1.00 C of excess charge on it. (b) What is unreasonable about this result? (c) Which assumptions are responsible?

Unreasonable Results

(a) Two 0.500 g raindrops in a thunderhead are 1.00 cm apart when they each acquire 1.00 mC charges. Find their acceleration. (b) What is unreasonable about this result? (c) Which premise or assumption is responsible?

Unreasonable Results

A wrecking yard inventor wants to pick up cars by charging a 0.400 m diameter ball and inducing an equal and opposite charge on the car. If a car has a 1000 kg mass and the ball is to be able to lift it from a distance of 1.00 m: (a) What minimum charge must be used? (b) What is the electric field near the surface of the ball? (c) Why are these results unreasonable? (d) Which premise or assumption is responsible?

Construct Your Own Problem

Consider two insulating balls with evenly distributed equal and opposite charges on their surfaces, held with a certain distance between the centers of the balls. Construct a problem in which you calculate the electric field (magnitude and direction) due to the balls at various points along a line running through the centers of the balls and extending to infinity on either side. Choose interesting points and comment on the meaning of the field at those points. For example, at what points might the field be just that due to one ball and where does the field become negligibly small? Among the things to be considered are the magnitudes of the charges and the distance between the centers of the balls. Your instructor may wish for you to consider the electric field off axis or for a more complex array of charges, such as those in a water molecule.

Construct Your Own Problem

Consider identical spherical conducting space ships in deep space where gravitational fields from other bodies are negligible compared to the gravitational attraction between the ships. Construct a problem in which you place identical excess charges on the space ships to exactly counter their gravitational attraction. Calculate the amount of excess charge needed. Examine whether that charge depends on the distance between the centers of the ships, the masses of the ships, or any other factors. Discuss whether this would be an easy, difficult, or even impossible thing to do in practice.