1. Home
  2. Fundamentals of electrical
  3. Information communication
  4. Wireline channels

6.2 Wireline channels  (Page 5/3)

<< Chapter < Page
  Fundamentals of electrical     Page 1 / 3
Chapter >> Page >
The analysis and transfer characteristics of wireline channels.

Wireline channels were the first used for electrical communications in the mid-nineteenth century for the telegraph.Here, the channel is one of several wires connecting transmitter to receiver. The transmitter simply creates a voltage relatedto the message signal and applies it to the wire(s). We must have a circuit—a closed path—that supports current flow. In thecase of single-wire communications, the earth is used as the current's return path. In fact, the term ground for the reference node in circuits originated in single-wire telegraphs. You can imagine that the earth's electricalcharacteristics are highly variable, and they are. Single-wire metallic channels cannot support high-quality signaltransmission having a bandwidth beyond a few hundred Hertz over any appreciable distance.

Coaxial cable cross-section

Coaxial cable consists of one conductor wrapped around the central conductor. This type of cable supports broaderbandwidth signals than twisted pair, and finds use in cable television and Ethernet.

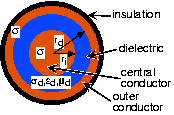
Consequently, most wireline channels today essentially consist of pairs of conducting wires ( [link] ), and the transmitter applies a message-related voltage across the pair. How these pairs of wires arephysically configured greatly affects their transmission characteristics. One example is twisted pair , wherein the wires are wrapped about each other. Telephonecables are one example of a twisted pair channel. Another is coaxial cable , where a concentric conductor surrounds a central wire with a dielectric material in between.Coaxial cable, fondly called "co-ax" by engineers, is what Ethernet uses as its channel. In either case, wireline channelsform a dedicated circuit between transmitter and receiver. As we shall find subsequently, several transmissions can share thecircuit by amplitude modulation techniques; commercial cable TV is an example. These information-carrying circuits are designedso that interference from nearby electromagnetic sources is minimized. Thus, by the time signals arrive at the receiver,they are relatively interference- and noise-free.

Both twisted pair and co-ax are examples of transmission lines , which all have the circuit model shown in [link] for an infinitesimally small length. This circuit model arisesfrom solving Maxwell's equations for the particular transmission line geometry.

Circuit model for a transmission line

The so-called distributed parameter model for two-wire cables has the depicted circuit model structure. Element valuesdepend on geometry and the properties of materials used to construct the transmission line.
The series resistance comes from the conductor used in the wires and from the conductor's geometry.The inductance and the capacitance derive from transmission line geometry, and the parallel conductance from the medium betweenthe wire pair. Note that all the circuit elements have values expressed by the product of a constant times a length; thisnotation represents that element values here have per-unit-length units. For example, the series resistance R ∼ has units of ohms/meter. For coaxial cable, the element values depend on the inner conductor's radius r i , the outer radius of the dielectric r d , the conductivity of the conductors σ , and the conductivity σ d , dielectric constant ε d , and magnetic permittivity μ d of the dielectric as
R ∼ 1 2 δ σ 1 r d 1 r i
C ∼ 2 ε d r d r i G ∼ 2 σ d r d r i L ∼ μ d 2 r d r i For twisted pair, having a separation d between the conductors that have conductivity σ and common radius r and that are immersed in a medium having dielectric and magnetic properties, the elementvalues are then
R ∼ 1 r δ σ
C ∼ ε d 2 r G ∼ σ d 2 r L ∼ μ δ 2 r d 2 r

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Fundamentals of electrical engineering i. OpenStax CNX. Aug 06, 2008 Download for free at http://legacy.cnx.org/content/col10040/1.9
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Fundamentals of electrical engineering i' conversation and receive update notifications?

Ask