6.1 Work: the scientific definition  (Page 8/5)

What it means to do work

The scientific definition of work differs in some ways from its everyday meaning. Certain things we think of as hard work, such as writing an exam or carrying a heavy load on level ground, are not work as defined by a scientist. The scientific definition of work reveals its relationship to energy—whenever work is done, energy is transferred.

For work, in the scientific sense, to be done, a force must be exerted and there must be motion or displacement in the direction of the force.

Formally, the work    done on a system by a constant force is defined to be the product of the component of the force in the direction of motion times the distance through which the force acts . For one-way motion in one dimension, this is expressed in equation form as

where $W$ is work, $\mathbf{d}$ is the displacement of the system, and $\theta$ is the angle between the force vector $\mathbf{F}$ and the displacement vector $\mathbf{d}$ , as in [link] . We can also write this as

To find the work done on a system that undergoes motion that is not one-way or that is in two or three dimensions, we divide the motion into one-way one-dimensional segments and add up the work done over each segment.

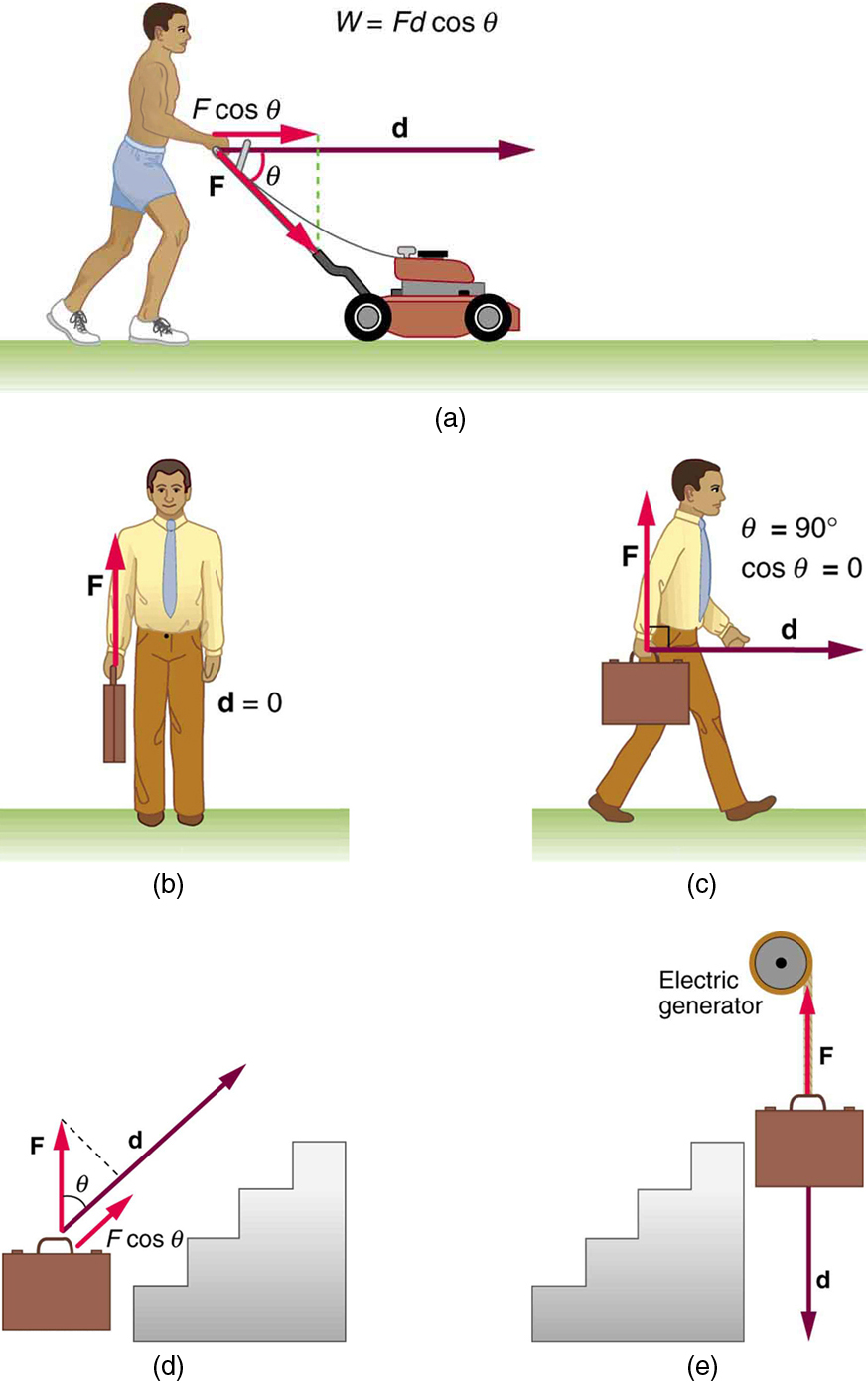
To examine what the definition of work means, let us consider the other situations shown in [link] . The person holding the briefcase in [link] (b) does no work, for example. Here $d=0$ , so $W=0$ . Why is it you get tired just holding a load? The answer is that your muscles are doing work against one another, but they are doing no work on the system of interest (the “briefcase-Earth system”—see Gravitational Potential Energy for more details). There must be motion for work to be done, and there must be a component of the force in the direction of the motion. For example, the person carrying the briefcase on level ground in [link] (c) does no work on it, because the force is perpendicular to the motion. That is, $\text{cos}\text{90}\text{º =}0$ , and so $W=0$ .