1. Home
  2. Introductory physics - for kpu
  3. Uniform circular motion and
  4. Centripetal acceleration

6.1 Centripetal acceleration  (Page 3/5)

<< Chapter < Page
  Introductory physics - for kpu     Page 3 / 5
Chapter >> Page >

Taking the age of Earth to be about 4 × 10 9 size 12{4 times "10" rSup { size 8{9} } } {} years and assuming its orbital radius of 1.5 × 10 11 size 12{4 times "10" rSup { size 8{9} } } {} has not changed and is circular, calculate the approximate total distance Earth has traveled since its birth (in a frame of reference stationary with respect to the Sun).

4 × 10 21 m size 12{ {underline {4 times "10" rSup { size 8{"21"} } " m"}} } {}

An ordinary workshop grindstone has a radius of 7.50 cm and rotates at 6500 rev/min.

(a) Calculate the magnitude of the centripetal acceleration at its edge in meters per second squared and convert it to multiples of g .

(b) What is the linear speed of a point on its edge?

a) 3 . 47 × 10 4 m / s 2 size 12{3 cdot "47" times "10" rSup { size 8{"4"} } m/s rSup { size 8{2} } } {} , 3 . 55 × 10 3 g size 12{3 cdot "55" times "10" rSup { size 8{"3"} } g} {}

b) 51 . 1 m / s size 12{3 cdot "75" m/s} {}

Helicopter blades withstand tremendous stresses. In addition to supporting the weight of a helicopter, they are spun at rapid rates and experience large centripetal accelerations, especially at the tip.

(a) Calculate the magnitude of the centripetal acceleration at the tip of a 4.00 m long helicopter blade that rotates at 300 rev/min.

(b) Compare the linear speed of the tip with the speed of sound (taken to be 340 m/s).

Verify that the linear speed of an ultracentrifuge is about 0.50 km/s, and Earth in its orbit is about 30 km/s by calculating:

(a) The linear speed of a point on an ultracentrifuge 0.100 m from its center, rotating at 50,000 rev/min.

(b) The linear speed of Earth in its orbit about the Sun (use data from the text on the radius of Earth’s orbit and approximate it as being circular).

a) 0.524 km/s

b) 29.7 km/s

At takeoff, a commercial jet has a 60.0 m/s speed. Its tires have a diameter of 0.850 m.

(a) At how many rev/min are the tires rotating?

(b) What is the centripetal acceleration at the edge of the tire?

(c) With what force must a determined 1 . 00 × 10 − 15 kg size 12{1 "." "00" times "10" rSup { size 8{ - "15"} } } {} bacterium cling to the rim?

(d) Take the ratio of this force to the bacterium’s weight.

(a) 1.35 × 10 3 rpm

(b) 8.47 × 10 3 m/s 2

(c) 8.47 × 10 –12 N

(d) 865

Integrated Concepts

Riders in an amusement park ride shaped like a Viking ship hung from a large pivot are rotated back and forth like a rigid pendulum. Sometime near the middle of the ride, the ship is momentarily motionless at the top of its circular arc. The ship then swings down under the influence of gravity.

(a) Assuming negligible friction, find the speed of the riders at the bottom of its arc, given the system's center of mass travels in an arc having a radius of 14.0 m and the riders are near the center of mass.

(b) What is the centripetal acceleration at the bottom of the arc?

(c) Draw a free body diagram of the forces acting on a rider at the bottom of the arc.

(d) Find the force exerted by the ride on a 60.0 kg rider and compare it to her weight.

(e) Discuss whether the answer seems reasonable.

(a) 16.6 m/s

(b) 19.6 m / s 2 alignl { stack { size 12{a \) " 16" cdot "6 " {m} slash {s} } {} #size 12{b \) " 19" cdot "6 " {m} slash {s rSup { size 8{2} } } } {} } } {}

(c)

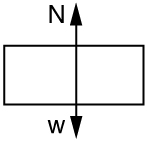
A rectangle with a base longer than the height. A vertical line with arrowheads on both ends passes through the rectangle, bisecting the horizontal sides. The top of the arrow is labeled N, and the bottom is labeled w.

(d) 1 . 76 × 10 3 N or 3 . 00 w size 12{" 1" cdot "76" times "10" rSup { size 8{3} } " N or 3" cdot "00 "w} {} , that is, the normal force (upward) is three times her weight.

(e) This answer seems reasonable, since she feels like she’s being forced into the chair MUCH stronger than just by gravity.

Unreasonable Results

A mother pushes her child on a swing so that his speed is 9.00 m/s at the lowest point of his path. The swing is suspended 2.00 m above the child’s center of mass.

(a) What is the magnitude of the centripetal acceleration of the child at the low point?

(b) What is the magnitude of the force the child exerts on the seat if his mass is 18.0 kg?

(c) What is unreasonable about these results?

(d) Which premises are unreasonable or inconsistent?

a) 40 . 5 m / s 2

b) 905 N

c) The force in part (b) is very large. The acceleration in part (a) is too much, about 4 g.

d) The speed of the swing is too large. At the given velocity at the bottom of the swing, there is enough kinetic energy to send the child all the way over the top, ignoring friction.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Introductory physics - for kpu phys 1100 (2015 edition). OpenStax CNX. May 30, 2015 Download for free at http://legacy.cnx.org/content/col11588/1.13
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Introductory physics - for kpu phys 1100 (2015 edition)' conversation and receive update notifications?

Ask