1. Home
  2. Abe advanced level physics
  3. Work, energy, and energy resources
  4. World energy use

5.8 World energy use  (Page 3/6)

<< Chapter < Page
  Abe advanced level physics     Page 3 / 6
Chapter >> Page >

Since energy in an isolated system is not destroyed or created or generated, one might wonder why we need to be concerned about our energy resources, since energy is a conserved quantity. The problem is that the final result of most energy transformations is waste heat transfer to the environment and conversion to energy forms no longer useful for doing work. To state it in another way, the potential for energy to produce useful work has been “degraded” in the energy transformation. (This will be discussed in more detail in Thermodynamics .)

Section summary

  • The relative use of different fuels to provide energy has changed over the years, but fuel use is currently dominated by oil, although natural gas and solar contributions are increasing.
  • Although non-renewable sources dominate, some countries meet a sizeable percentage of their electricity needs from renewable resources.
  • The United States obtains only about 10% of its energy from renewable sources, mostly hydroelectric power.
  • Economic well-being is dependent upon energy use, and in most countries higher standards of living, as measured by GDP (Gross Domestic Product) per capita, are matched by higher levels of energy consumption per capita.
  • Even though, in accordance with the law of conservation of energy, energy can never be created or destroyed, energy that can be used to do work is always partly converted to less useful forms, such as waste heat to the environment, in all of our uses of energy for practical purposes.

Conceptual questions

What is the difference between energy conservation and the law of conservation of energy? Give some examples of each.

If the efficiency of a coal-fired electrical generating plant is 35%, then what do we mean when we say that energy is a conserved quantity?

Problems&Exercises

Integrated Concepts

(a) Calculate the force the woman in [link] exerts to do a push-up at constant speed, taking all data to be known to three digits. (b) How much work does she do if her center of mass rises 0.240 m? (c) What is her useful power output if she does 25 push-ups in 1 min? (Should work done lowering her body be included? See the discussion of useful work in Work, Energy, and Power in Humans .

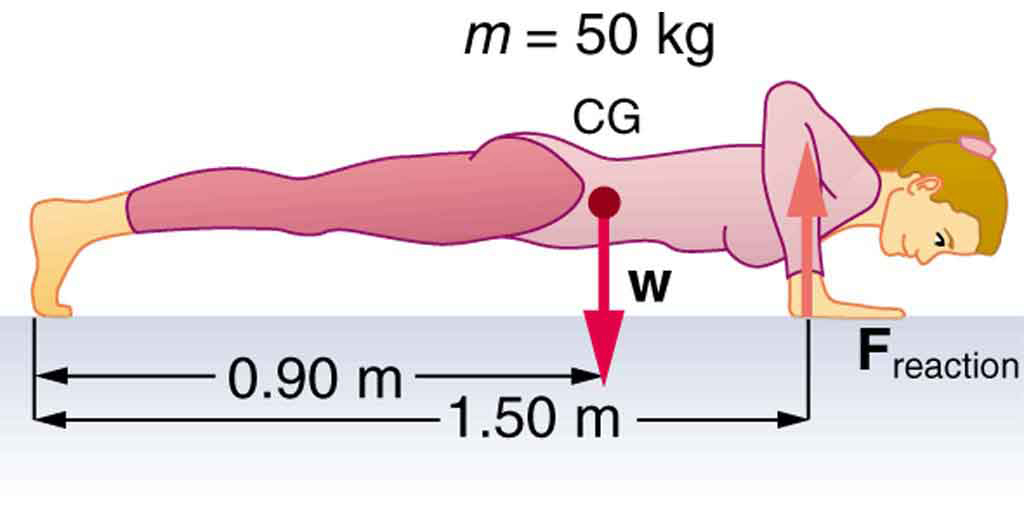
A woman is doing push-ups. Her weight w is acting on her center of gravity , shown by a vector pointing downwards. Her center of gravity is zero point nine zero meters from her feet and reaction force F acting on her arms is shown by the vector pointing upward along her arms. The distance of reaction force from the feet is one point five zero meters.
Forces involved in doing push-ups. The woman’s weight acts as a force exerted downward on her center of gravity (CG).

(a) 294 N

(b) 118 J

(c) 49.0 W

Integrated Concepts

A 75.0-kg cross-country skier is climbing a 3 . 0º size 12{3 "." 0°} {} slope at a constant speed of 2.00 m/s and encounters air resistance of 25.0 N. Find his power output for work done against the gravitational force and air resistance. (b) What average force does he exert backward on the snow to accomplish this? (c) If he continues to exert this force and to experience the same air resistance when he reaches a level area, how long will it take him to reach a velocity of 10.0 m/s?

Integrated Concepts

The 70.0-kg swimmer in [link] starts a race with an initial velocity of 1.25 m/s and exerts an average force of 80.0 N backward with his arms during each 1.80 m long stroke. (a) What is his initial acceleration if water resistance is 45.0 N? (b) What is the subsequent average resistance force from the water during the 5.00 s it takes him to reach his top velocity of 2.50 m/s? (c) Discuss whether water resistance seems to increase linearly with velocity.

(a) 0.500 m /s 2 size 12{0 "." "500"" m/s" rSup { size 8{2} } } {}

(b) 62.5 N

(c) Assuming the acceleration of the swimmer decreases linearly with time over the 5.00 s interval, the frictional force must therefore be increasing linearly with time, since f = F − ma size 12{f=F - ital "ma"} {} . If the acceleration decreases linearly with time, the velocity will contain a term dependent on time squared ( t 2 size 12{t rSup { size 8{2} } } {} ). Therefore, the water resistance will not depend linearly on the velocity.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Abe advanced level physics. OpenStax CNX. Jul 11, 2013 Download for free at http://legacy.cnx.org/content/col11534/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Abe advanced level physics' conversation and receive update notifications?

Ask