5.7 Poisson

The average number of loaves of bread put on a shelf in a bakery in a half-hour period is 12. Of interest is the number of loaves of bread put on the shelf in 5 minutes. Thetime interval of interest is 5 minutes. What is the probability that the number of loaves, selected randomly, put on the shelf in 5 minutes is 3?

Let $X$ = the number of loaves of bread put on the shelf in 5 minutes. If the average number of loaves put on the shelf in 30 minutes (half-hour) is 12, then the average number of loaves put on the shelf in 5 minutes is

$\left(\frac{5}{30}\right)\cdot 12=2$ loaves of bread

The probability question asks you to find $\mathrm{P(x\; =\; 3)}$ .

A certain bank expects to receive 6 bad checks per day, on average. What is the probability of the bank getting fewer than 5 bad checks on any given day? Of interestis the number of checks the bank receives in 1 day, so the time interval of interest is 1 day. Let $X$ = the number of bad checks the bank receives in one day. If the bank expects to receive 6 bad checks per day then the average is 6 checks per day.The probability question asks for $P(x< 5)$ .

You notice that a news reporter says "uh", on average, 2 times per broadcast. What is the probability that the news reporter says "uh" more than 2 times per broadcast.

This is a Poisson problem because you are interested in knowing the number of times the news reporter says "uh" during a broadcast.

Leah's answering machine receives about 6 telephone calls between 8 a.m. and 10 a.m. What is the probability that Leah receives more than 1 call in the next 15 minutes?

Let $X$ = the number of calls Leah receives in 15 minutes. (The interval of interest is 15 minutes or $\frac{1}{4}$ hour.)

$x$ = 0, 1, 2, 3, ...

If Leah receives, on the average, 6 telephone calls in 2 hours, and there are eight 15 minutes intervals in 2 hours, then Leah receives

$\frac{1}{8}\cdot 6=0.75$

calls in 15 minutes, on the average. So, $\mu$ = 0.75 for this problem.

$X$ ~ $\text{P(0.75)}$

Find $P(x> 1)$ . $P(x> 1)=0.1734$ (calculator or computer)

TI-83+ and TI-84: For a general discussion, see this example (Binomial) . The syntax is similar. The Poisson parameter list is ( $\mu$ for the interval of interest, number). For this problem:

Press 1- and then press 2nd DISTR. Arrow down to C:poissoncdf. Press ENTER. Enter .75,1). The result is $P(x> 1)=0.1734$ . NOTE: The TI calculators use $\lambda$ (lambda) for the mean.

The probability that Leah receives more than 1 telephone call in the next fifteen minutes is about 0.1734.

The graph of $X$ ~ $\text{P(0.75)}$ is:

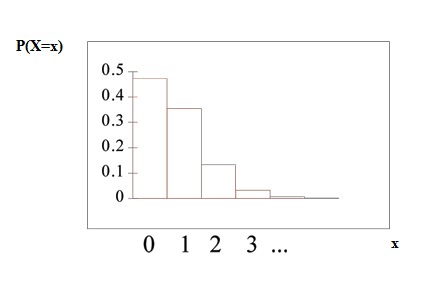
The y-axis contains the probability of $x$ where $X$ = the number of calls in 15 minutes.