| << Chapter < Page | Chapter >> Page > |
Recall from Substitution Rule the method of integration by substitution. When evaluating an integral such as we substitute Then or and the limits change to and Thus the integral becomes and this integral is much simpler to evaluate. In other words, when solving integration problems, we make appropriate substitutions to obtain an integral that becomes much simpler than the original integral.
We also used this idea when we transformed double integrals in rectangular coordinates to polar coordinates and transformed triple integrals in rectangular coordinates to cylindrical or spherical coordinates to make the computations simpler. More generally,
Where and and satisfy and
A similar result occurs in double integrals when we substitute and Then we get
where the domain is replaced by the domain in polar coordinates. Generally, the function that we use to change the variables to make the integration simpler is called a transformation or mapping.
A planar transformation is a function that transforms a region in one plane into a region in another plane by a change of variables. Both and are subsets of For example, [link] shows a region in the transformed into a region in the by the change of variables and or sometimes we write and We shall typically assume that each of these functions has continuous first partial derivatives, which means and exist and are also continuous. The need for this requirement will become clear soon.
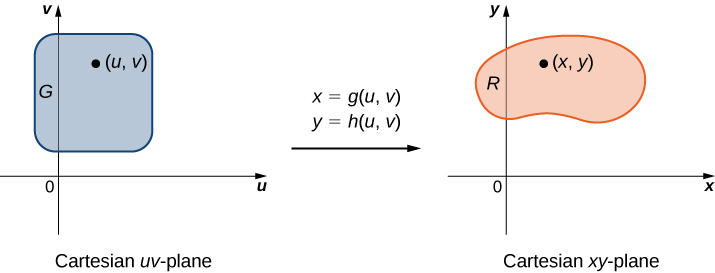
A transformation defined as is said to be a one-to-one transformation if no two points map to the same image point.
To show that is a one-to-one transformation, we assume and show that as a consequence we obtain If the transformation is one-to-one in the domain then the inverse exists with the domain such that and are identity functions.
[link] shows the mapping where and are related to and by the equations and The region is the domain of and the region is the range of also known as the image of under the transformation
Suppose a transformation is defined as where Find the image of the polar rectangle in the to a region in the Show that is a one-to-one transformation in and find
Since varies from 0 to 1 in the we have a circular disc of radius 0 to 1 in the Because varies from 0 to in the we end up getting a quarter circle of radius in the first quadrant of the ( [link] ). Hence is a quarter circle bounded by in the first quadrant.
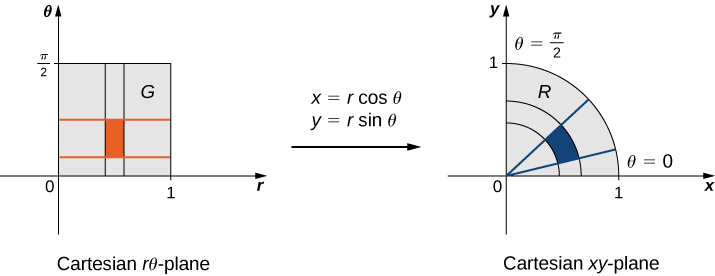
In order to show that is a one-to-one transformation, assume and show as a consequence that In this case, we have
Dividing, we obtain
since the tangent function is one-one function in the interval Also, since we have Therefore, and is a one-to-one transformation from into
To find solve for in terms of We already know that and Thus is defined as and

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?