5.6 Hypergeometric (optional)

A candy dish contains 100 jelly beans and 80 gumdrops. Fifty candies are picked at random. What is the probability that 35 of the 50 are gumdrops? The two groupsare jelly beans and gumdrops. Since the probability question asks for the probability of picking gumdrops, the group of interest (first group) is gumdrops. The size of the group of interest (firstgroup) is 80. The size of the second group is 100. The size of the sample is 50 (jelly beans or gumdrops). Let $X$ = the number of gumdrops in the sample of 50. $X$ takes on the values $x$ = 0, 1, 2, ..., 50. The probability question is $P(x=35)$ .

Suppose a shipment of 100 VCRs is known to have 10 defective VCRs. An inspector randomly chooses 12 for inspection. He is interested in determining the probability that,among the 12, at most 2 are defective. The two groups are the 90 non-defective VCRs and the 10 defective VCRs. The group of interest (first group) is the defective group becausethe probability question asks for the probability of at most 2 defective VCRs. The size of the sample is 12 VCRs. (They may be non-defective or defective.) Let $X$ = the number of defective VCRs in the sample of 12. $X$ takes on the values 0, 1, 2, ..., 10. $X$ may not take on the values 11 or 12. The sample size is 12, but there are only 10 defective VCRs. Theinspector wants to know $P(x\le 2)$ ("At most" means "less than or equal to").

You are president of an on-campus special events organization. You need a committee of 7 to plan a special birthday party for the president of the college. Yourorganization consists of 18 women and 15 men. You are interested in the number of men on your committee. If the members of the committee are randomly selected, what is the probability that your committee has more than 4 men?

This is a hypergeometric problem because you are choosing your committee from two groups (men and women).

A school site committee is to be chosen randomly from 6 men and 5 women. If the committee consists of 4 members chosen randomly, what is the probability that 2 of themare men? How many men do you expect to be on the committee?

Let $X$ = the number of men on the committee of 4. The men are the group of interest (first group).

$X$ takes on the values 0, 1, 2, 3, 4, where $r=6$ , $b=5$ , and $n=4$ . $X~\mathrm{H(6,\; 5,\; 4)}$

Find $P(x=2)$ . $P(x=2)=0.4545$ (calculator or computer)

The probability that there are 2 men on the committee is about 0.45.

The graph of $X$ ~ $\mathrm{H(6,\; 5,\; 4)}$ is:

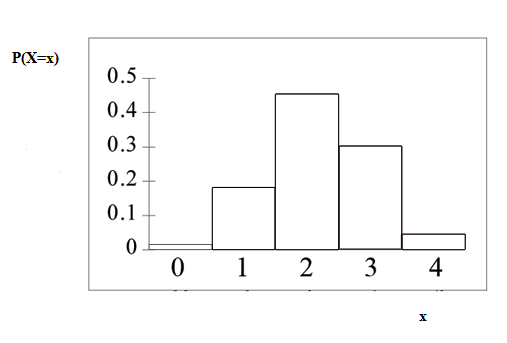
The $y$ -axis contains the probability of $X$ , where $X$ = the number of men on thecommittee.

You would expect $m=\mathrm{2.18}$ (about 2) men on the committee.

The formula for the mean is $\mu =\frac{n\cdot r}{r+b}=\frac{4\cdot 6}{6+5}=2.18$

The formula for the variance is fairly complex. You will find it in the Summary of the Discrete Probability Functions Chapter .