5.6 Calculating centers of mass and moments of inertia  (Page 12/8)

We have already discussed a few applications of multiple integrals, such as finding areas, volumes, and the average value of a function over a bounded region. In this section we develop computational techniques for finding the center of mass and moments of inertia of several types of physical objects, using double integrals for a lamina (flat plate) and triple integrals for a three-dimensional object with variable density. The density is usually considered to be a constant number when the lamina or the object is homogeneous; that is, the object has uniform density.

Center of mass in two dimensions

The center of mass is also known as the center of gravity if the object is in a uniform gravitational field. If the object has uniform density, the center of mass is the geometric center of the object, which is called the centroid. [link] shows a point $P$ as the center of mass of a lamina. The lamina is perfectly balanced about its center of mass.

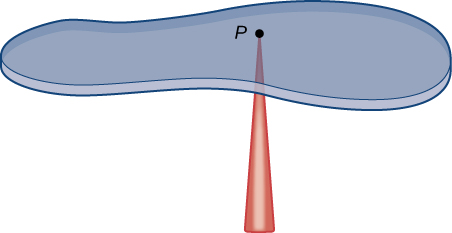
To find the coordinates of the center of mass $P(\stackrel{\text{−}}{x},\stackrel{\text{−}}{y})$ of a lamina, we need to find the moment $M_x$ of the lamina about the $x\text{-axis}$ and the moment $M_y$ about the $y\text{-axis}\text{.}$ We also need to find the mass $m$ of the lamina. Then

Refer to Moments and Centers of Mass for the definitions and the methods of single integration to find the center of mass of a one-dimensional object (for example, a thin rod). We are going to use a similar idea here except that the object is a two-dimensional lamina and we use a double integral.

If we allow a constant density function, then $\stackrel{\text{−}}{x}=\frac{M_y}{m}\text{and}\stackrel{\text{−}}{y}=\frac{M_x}{m}$ give the centroid of the lamina.

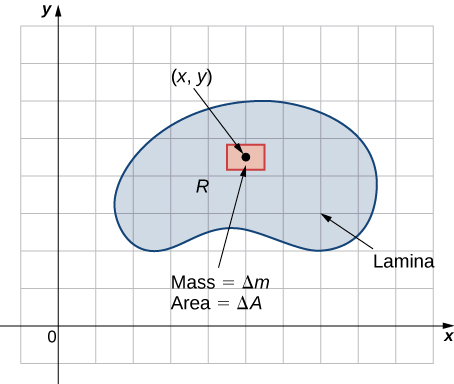
Suppose that the lamina occupies a region $R$ in the $xy\text{-plane},$ and let $\rho \left(x,y\right)$ be its density (in units of mass per unit area) at any point $\left(x,y\right).$ Hence, $\rho \left(x,y\right)=\underset{\text{Δ}A\to 0}{\text{lim}}\frac{\text{Δ}m}{\text{Δ}A},$ where $\text{Δ}m$ and $\text{Δ}A$ are the mass and area of a small rectangle containing the point $\left(x,y\right)$ and the limit is taken as the dimensions of the rectangle go to $0$ (see the following figure).

Just as before, we divide the region $R$ into tiny rectangles $R_{ij}$ with area $\text{Δ}A$ and choose $\left(x_{ij}^{*},y_{ij}^{*}\right)$ as sample points. Then the mass $m_{ij}$ of each $R_{ij}$ is equal to $\rho \left(x_{ij}^{*},y_{ij}^{*}\right)\text{Δ}A$ ( [link] ). Let $k$ and $l$ be the number of subintervals in $x$ and $y,$ respectively. Also, note that the shape might not always be rectangular but the limit works anyway, as seen in previous sections.

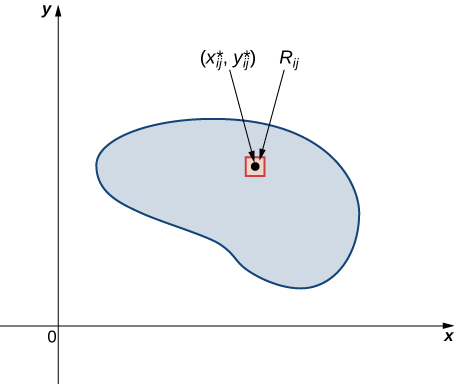
Hence, the mass of the lamina is

Let’s see an example now of finding the total mass of a triangular lamina.

Finding the total mass of a lamina

Consider a triangular lamina $R$ with vertices $\left(0,0\right),\left(0,3\right),$ $\left(3,0\right)$ and with density $\rho \left(x,y\right)=xy{\text{kg/m}}^2.$ Find the total mass.

A sketch of the region $R$ is always helpful, as shown in the following figure.

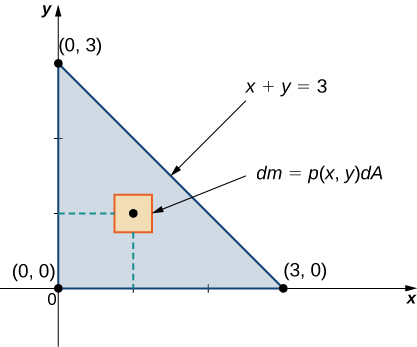
Using the expression developed for mass, we see that

$\begin{array}{cc}\hfill m& ={\displaystyle \underset{R}{\iint }dm={\displaystyle \underset{R}{\iint }\rho \left(x,y\right)}}dA={\displaystyle \underset{x=0}{\overset{x=3}{\int }}{\displaystyle \underset{y=0}{\overset{y=3-x}{\int }}xydydx={\displaystyle \underset{x=0}{\overset{x=3}{\int }}\left[{x\frac{y^2}{2}|}_{y=0}^{y=3-x}\right]}}}dx\hfill \\ & ={\displaystyle \underset{x=0}{\overset{x=3}{\int }}\frac{1}{2}}x{\left(3-x\right)}^{2}dx={\left[\frac{9x^2}{4}-x^3+\frac{x^4}{8}\right]|}_{x=0}^{x=3}\hfill \\ & =\frac{27}{8}.\hfill \end{array}$

The computation is straightforward, giving the answer $m=\frac{27}{8}\text{kg}\text{.}$

Got questions? Get instant answers now!

Got questions? Get instant answers now!