5.5 Sound interference and resonance: standing waves in air columns  (Page 2/11)

Suppose we hold a tuning fork near the end of a tube that is closed at the other end, as shown in [link] , [link] , [link] , and [link] . If the tuning fork has just the right frequency, the air column in the tube resonates loudly, but at most frequencies it vibrates very little. This observation just means that the air column has only certain natural frequencies. The figures show how a resonance at the lowest of these natural frequencies is formed. A disturbance travels down the tube at the speed of sound and bounces off the closed end. If the tube is just the right length, the reflected sound arrives back at the tuning fork exactly half a cycle later, and it interferes constructively with the continuing sound produced by the tuning fork. The incoming and reflected sounds form a standing wave in the tube as shown.

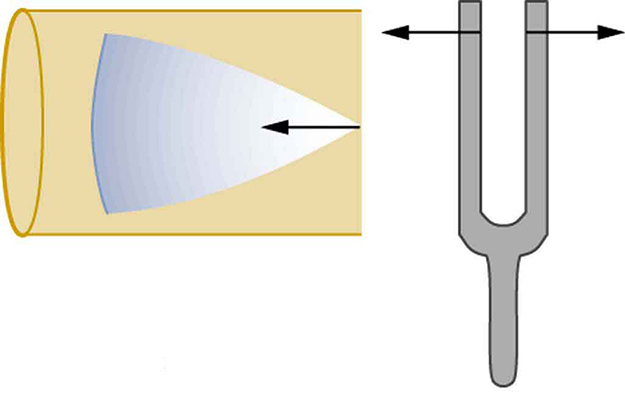
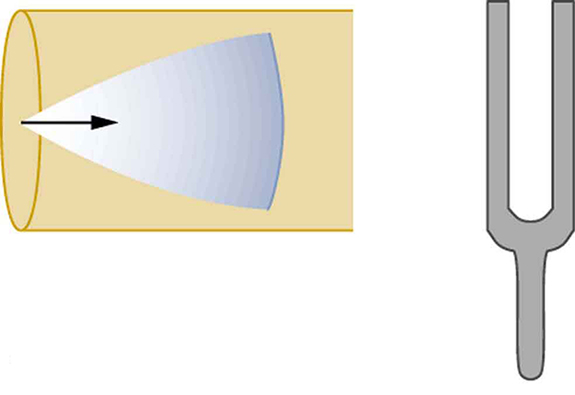
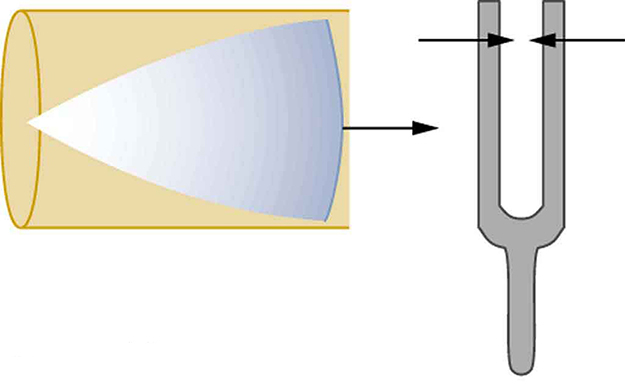
The standing wave formed in the tube has its maximum air displacement (an antinode    ) at the open end, where motion is unconstrained, and no displacement (a node    ) at the closed end, where air movement is halted. The distance from a node to an antinode is one-fourth of a wavelength, and this equals the length of the tube; thus, $\lambda =4L$ . This same resonance can be produced by a vibration introduced at or near the closed end of the tube, as shown in [link] . It is best to consider this a natural vibration of the air column independently of how it is induced.

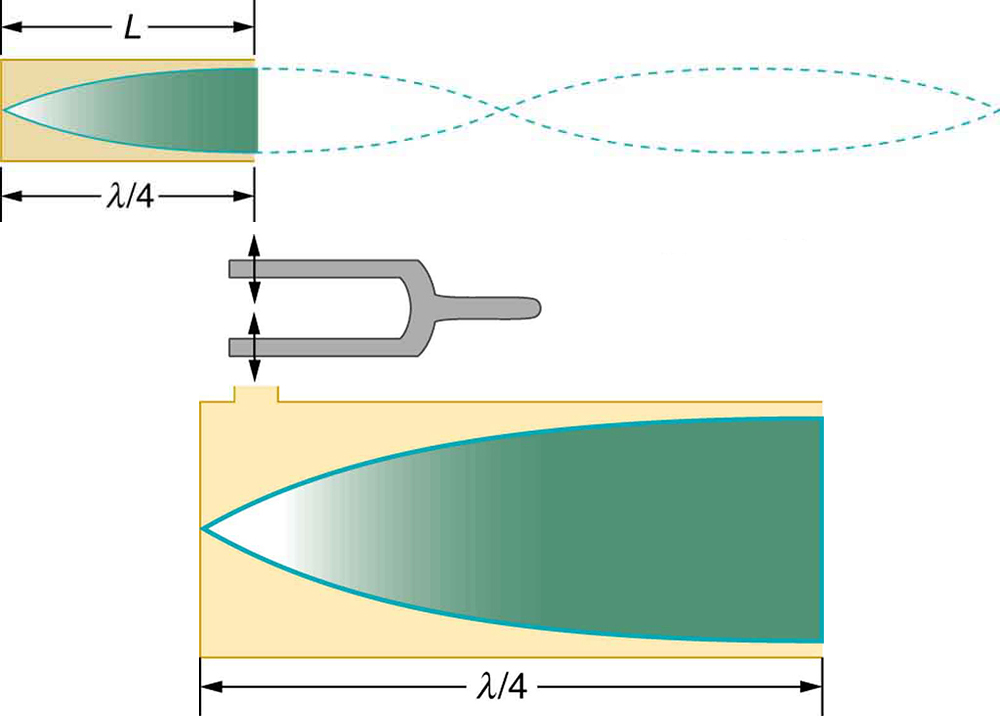
Given that maximum air displacements are possible at the open end and none at the closed end, there are other, shorter wavelengths that can resonate in the tube, such as the one shown in [link] . Here the standing wave has three-fourths of its wavelength in the tube, or $L=(3/4)\lambda \prime$ , so that $\lambda \prime =4L/3$ . Continuing this process reveals a whole series of shorter-wavelength and higher-frequency sounds that resonate in the tube. We use specific terms for the resonances in any system. The lowest resonant frequency is called the fundamental    , while all higher resonant frequencies are called overtones    . All resonant frequencies are integral multiples of the fundamental, and they are collectively called harmonics    . The fundamental is the first harmonic, the first overtone is the second harmonic, and so on. [link] shows the fundamental and the first three overtones (the first four harmonics) in a tube closed at one end.