| << Chapter < Page | Chapter >> Page > |
Thus far, all equations that have been encountered have one unknown variable that must be solved for. When two unknown variables need to be solved for, two equations are required and these equations are known as simultaneous equations. The solutions to the system of simultaneous equations are the values of the unknown variables which satisfy the system of equations simultaneously, that means at the same time. In general, if there are unknown variables, then equations are required to obtain a solution for each of the variables.
An example of a system of simultaneous equations is:
In order to find a numerical value for an unknown variable, one must have at least as many independent equations as variables. We solve simultaneous equations graphically and algebraically.
Khan academy video on simultaneous equations - 1
Simultaneous equations can be solved graphically. If the graph corresponding to each equation is drawn, then the solution to the system of simultaneous equations is the co-ordinate of the point at which both graphs intersect.
Draw the graphs of the two equations in [link] .
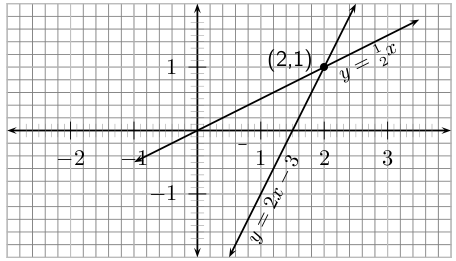
The intersection of the two graphs is . So the solution to the system of simultaneous equations in [link] is and .
This can be shown algebraically as:
Solve the following system of simultaneous equations graphically.
For the first equation:
and for the second equation:
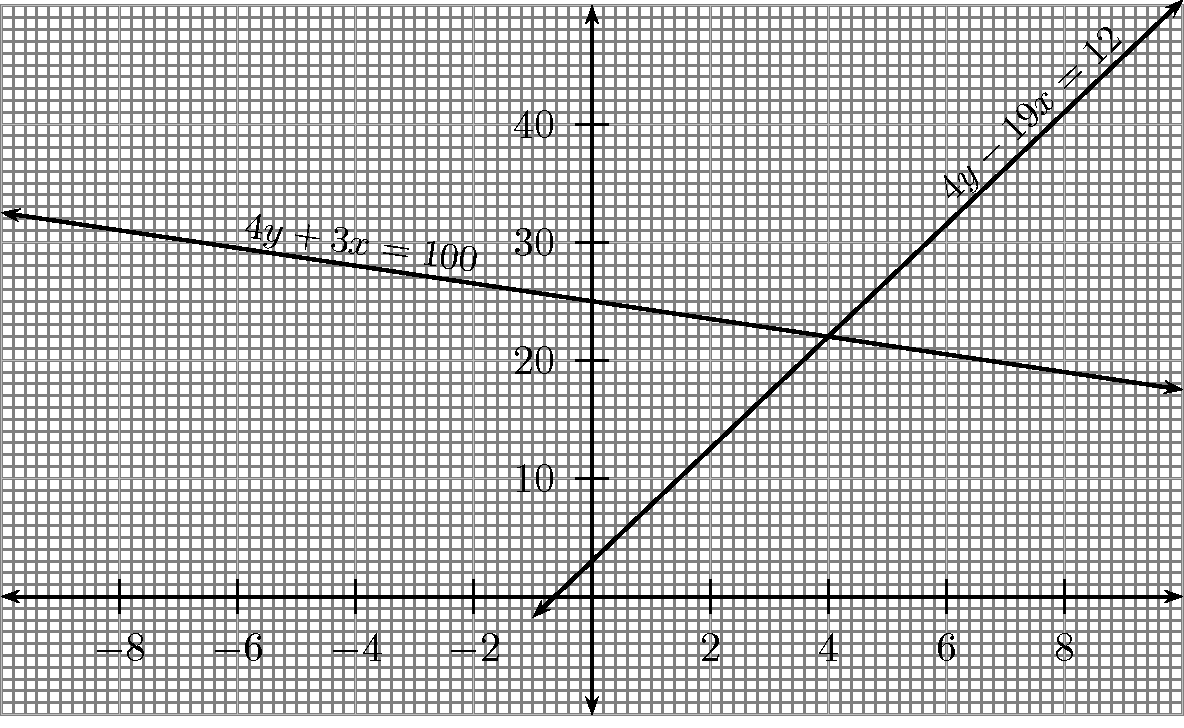
The graphs intersect at .
A common algebraic technique is the substitution method: try to solve one of the equations for one of the variables and substitute the result into the other equations, thereby reducing the number of equations and the number of variables by 1. Continue until you reach a single equation with a single variable, which (hopefully) can be solved; back substitution then allows checking the values for the other variables.
In the example [link] , we first solve the first equation for :
and substitute this result into the second equation:
The solution for the system of simultaneous equations [link] is:
Solve the following system of simultaneous equations:
A shop sells bicycles and tricycles. In total there are 7 cycles (cycles includes both bicycles and tricycles) and 19 wheels. Determine how many of each there are, if a bicycle has two wheels and a tricycle has three wheels.
The number of bicycles and the number of tricycles are required.
If is the number of bicycles and is the number of tricycles, then:

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [caps]' conversation and receive update notifications?