| << Chapter < Page | Chapter >> Page > |
We are familiar with a function of the form where is the function and is the argument. Examples are:
The basis of trigonometry are the trigonometric functions . There are three basic trigonometric functions:
These are abbreviated to:
These functions are defined from a right-angled triangle , a triangle where one internal angle is 90 .
Consider a right-angled triangle.

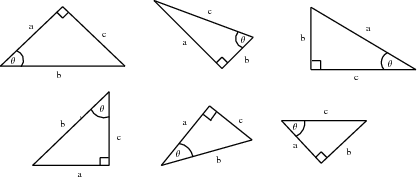
In the right-angled triangle, we refer to the lengths of the three sides according to how they are placed in relation to the angle . The side opposite to the right angle is labelled the hypotenus , the side opposite is labelled opposite , the side next to is labelled adjacent . Note that the choice of non-90 degree internal angle is arbitrary. You can choose either internal angle and then define the adjacent and opposite sides accordingly. However, the hypotenuse remains the same regardless of which internal angle you are referring to.
We define the trigonometric functions, also known as trigonometric identities, as:
These functions relate the lengths of the sides of a right-angled triangle to its interior angles.
One way of remembering the definitions is to use the following mnemonic that is perhaps easier to remember:
| S illy O ld H ens | |
| C ackle A nd H owl | |
| T ill O ld A ge |
You may also hear people saying Soh Cah Toa. This is just another way to remember the trig functions.
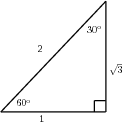

For most angles , it is very difficult to calculate the values of , and . One usually needs to use a calculator to do so. However, we saw in the above Activity that we could work these values out for some special angles. Some of these angles are listed in the table below, along with the values of the trigonometric functions at these angles. Remember that the lengths of the sides of a right angled triangle must obey Pythagoras' theorum. The square of the hypothenuse (side opposite the 90 degree angle) equals the sum of the squares of the two other sides.
| 1 | 0 | |||||
| 0 | 1 | 0 | ||||
| 0 | 1 | 0 |
These values are useful when asked to solve a problem involving trig functions without using a calculator.
Find the length of x in the following triangle.
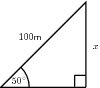
In this case you have an angle ( ), the opposite side and the hypotenuse.
So you should use
Use the sin button on your calculator
Find the value of in the following triangle.

In this case you have the opposite side and the hypotenuse to the angle .
So you should use
Since you are finding the angle ,
use on your calculator
Don't forget to set your calculator to `deg' mode!
The following videos provide a summary of what you have learnt so far.
Trigonometry - 1
Khan academy video on trigonometry - 2
Find the length of the sides marked with letters. Give answers correct to 2 decimal places.



Notification Switch
Would you like to follow the 'Contemporary math applications' conversation and receive update notifications?