5.4 Cosine and sine identities  (Page 4/2)

Sine and cosine identities

There are a few identities relating to the trigonometric functions that make working with triangles easier. These are:

1. the sine rule
2. the cosine rule
3. the area rule

and will be described and applied in this section.

The sine rule

The Sine Rule

The sine rule applies to any triangle: $\frac{sin\widehat{A}}{a}=\frac{sin\widehat{B}}{b}=\frac{sin\widehat{C}}{c}$ where $a$ is the side opposite $\widehat{A}$ , $b$ is the side opposite $\widehat{B}$ and $c$ is the side opposite $\widehat{C}$ .

Consider $▵ABC$ .

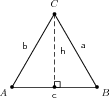
The area of $▵ABC$ can be written as: $\mathrm{area}▵\mathrm{ABC}=\frac{1}{2}\mathrm{c}·\mathrm{h}.$ However, $h$ can be calculated in terms of $\widehat{A}$ or $\widehat{B}$ as:

and

Therefore the area of $▵ABC$ is: $\frac{1}{2}c·h=\frac{1}{2}c·b·sin\widehat{A}=\frac{1}{2}c·a·sin\widehat{B}$

Similarly, by drawing the perpendicular between point $B$ and line $AC$ we can show that: $\frac{1}{2}c·b·sin\widehat{A}=\frac{1}{2}a·b·sin\widehat{C}$

Therefore the area of $▵ABC$ is: $\frac{1}{2}c·b·sin\widehat{A}=\frac{1}{2}c·a·sin\widehat{B}=\frac{1}{2}a·b·sin\widehat{C}$

If we divide through by $\frac{1}{2}a·b·c$ , we get: $\frac{sin\widehat{A}}{a}=\frac{sin\widehat{B}}{b}=\frac{sin\widehat{C}}{c}$

This is known as the sine rule and applies to any triangle, right angled or not.

There is a coastline with two lighthouses, one on either side of a beach. The two lighthouses are $0,67$  km apart and one is exactly due east of the other. The lighthouses tell how close a boat is by taking bearings to the boat (remember – a bearing is an angle measured clockwise from north). These bearings are shown. Use the sine rule to calculate how far the boat is from each lighthouse.

1. Determine what is given

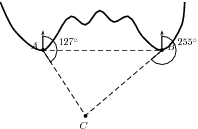
   We can see that the two lighthouses and the boat form a triangle. Since we know the distance between the lighthouses and we have two angles we can use trigonometry to find the remaining two sides of the triangle, the distance of the boat from the two lighthouses.

   

2. Determine what you need

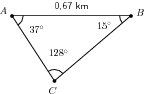
   We need to know the lengths of the two sides $\mathrm{AC}$ and $\mathrm{BC}$ . We can use the sine rule to find our missing lengths.

   $$\begin{array}{ccc}\hfill \frac{BC}{sin\widehat{A}}& =& \frac{AB}{sin\widehat{C}}\hfill \\ \hfill BC& =& \frac{AB·sin\widehat{A}}{sin\widehat{C}}\hfill \\ & =& \frac{(0,67\mathrm{km})sin\left({37}^{\circ }\right)}{sin\left({128}^{\circ }\right)}\hfill \\ & =& 0,51\mathrm{km}\hfill \end{array}$$
   $$\begin{array}{ccc}\hfill \frac{AC}{sin\widehat{B}}& =& \frac{AB}{sin\widehat{C}}\hfill \\ \hfill AC& =& \frac{AB·sin\widehat{B}}{sin\widehat{C}}\hfill \\ & =& \frac{(0,67\mathrm{km})sin\left({15}^{\circ }\right)}{sin\left({128}^{\circ }\right)}\hfill \\ & =& 0,22\mathrm{km}\hfill \end{array}$$

Sine rule

1. Show that $\frac{sin\widehat{A}}{a}=\frac{sin\widehat{B}}{b}=\frac{sin\widehat{C}}{c}$ is equivalent to: $\frac{a}{sin\widehat{A}}=\frac{b}{sin\widehat{B}}=\frac{c}{sin\widehat{C}}$ Note: either of these two forms can be used.
2. Find all the unknown sides and angles of the following triangles:
   1. $▵$ PQR in which $\widehat{\mathrm{Q}}={64}^{\circ }$ ; $\widehat{\mathrm{R}}={24}^{\circ }$ and $r=3$
   2. $▵$ KLM in which $\widehat{\mathrm{K}}={43}^{\circ }$ ; $\widehat{\mathrm{M}}={50}^{\circ }$ and $m=1$
   3. $▵$ ABC in which $\widehat{\mathrm{A}}=32,7^{\circ }$ ; $\widehat{\mathrm{C}}=70,5^{\circ }$ and $a=52,3$
   4. $▵$ XYZ in which $\widehat{\mathrm{X}}={56}^{\circ }$ ; $\widehat{\mathrm{Z}}={40}^{\circ }$ and $x=50$
3. In $▵$ ABC, $\widehat{\mathrm{A}}={116}^{\circ }$ ; $\widehat{\mathrm{C}}={32}^{\circ }$ and $\mathrm{AC}=23$  m. Find the length of the side AB.
4. In $▵$ RST, $\widehat{\mathrm{R}}={19}^{\circ }$ ; $\widehat{\mathrm{S}}={30}^{\circ }$ and $\mathrm{RT}=120$  km. Find the length of the side ST.
5. In $▵$ KMS, $\widehat{\mathrm{K}}={20}^{\circ }$ ; $\widehat{\mathrm{M}}={100}^{\circ }$ and $s=23$  cm. Find the length of the side m.

The cosine rule

The Cosine Rule

The cosine rule applies to any triangle and states that:

$$\begin{array}{ccc}\hfill a^2& =& b^2+c^2-2bccos\widehat{A}\hfill \\ \hfill b^2& =& c^2+a^2-2cacos\widehat{B}\hfill \\ \hfill c^2& =& a^2+b^2-2abcos\widehat{C}\hfill \end{array}$$

where $a$ is the side opposite $\widehat{A}$ , $b$ is the side opposite $\widehat{B}$ and $c$ is the side opposite $\widehat{C}$ .

The cosine rule relates the length of a side of a triangle to the angle opposite it and the lengths of the other two sides.

Consider $▵ABC$ which we will use to show that: $a^2=b^2+c^2-2bccos\widehat{A}.$

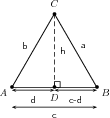
In $▵DCB$ : $a^2={(c-d)}^2+h^2$ from the theorem of Pythagoras.

In $▵ACD$ : $b^2=d^2+h^2$ from the theorem of Pythagoras.

We can eliminate $h^2$ from [link] and [link] to get:

In order to eliminate $d$ we look at $▵ACD$ , where we have: $cos\widehat{A}=\frac{d}{b}.$ So, $d=bcos\widehat{A}.$ Substituting this into [link] , we get: $a^2=b^2+c^2-2bccos\widehat{A}$