5.4 Carnot’s perfect heat engine: the second law of thermodynamics  (Page 3/7)

Strategy

Since temperatures are given for the hot and cold reservoirs of this heat engine, ${\mathrm{Eff}}_{\text{C}}=1-\frac{T_{\text{c}}}{T_{\text{h}}}$ can be used to calculate the Carnot (maximum theoretical) efficiency. Those temperatures must first be converted to kelvins.

Solution

The hot and cold reservoir temperatures are given as $\text{300}\text{º}\text{C}$ and $\text{27}\text{.}0\text{º}\text{C}$ , respectively. In kelvins, then, $T_{\text{h}}=\text{573 K}$ and $T_{\text{c}}=\text{300 K}$ , so that the maximum efficiency is

Thus,

Discussion

A typical nuclear power station’s actual efficiency is about 35%, a little better than 0.7 times the maximum possible value, a tribute to superior engineering. Electrical power stations fired by coal, oil, and natural gas have greater actual efficiencies (about 42%), because their boilers can reach higher temperatures and pressures. The cold reservoir temperature in any of these power stations is limited by the local environment. [link] shows (a) the exterior of a nuclear power station and (b) the exterior of a coal-fired power station. Both have cooling towers into which water from the condenser enters the tower near the top and is sprayed downward, cooled by evaporation.

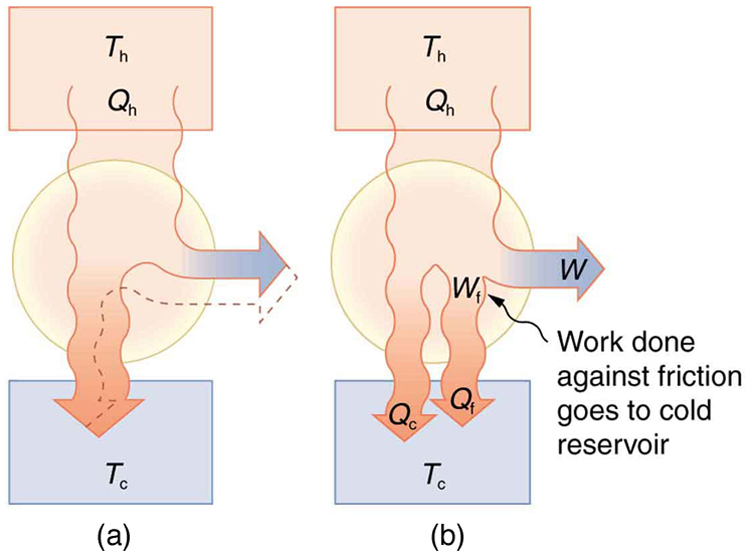
Since all real processes are irreversible, the actual efficiency of a heat engine can never be as great as that of a Carnot engine, as illustrated in [link] (a). Even with the best heat engine possible, there are always dissipative processes in peripheral equipment, such as electrical transformers or car transmissions. These further reduce the overall efficiency by converting some of the engine’s work output back into heat transfer, as shown in [link] (b).

Section summary

• The Carnot cycle is a theoretical cycle that is the most efficient cyclical process possible. Any engine using the Carnot cycle, which uses only reversible processes (adiabatic and isothermal), is known as a Carnot engine.
• Any engine that uses the Carnot cycle enjoys the maximum theoretical efficiency.
• While Carnot engines are ideal engines, in reality, no engine achieves Carnot’s theoretical maximum efficiency, since dissipative processes, such as friction, play a role. Carnot cycles without heat loss may be possible at absolute zero, but this has never been seen in nature.

Conceptual questions