| << Chapter < Page | Chapter >> Page > |
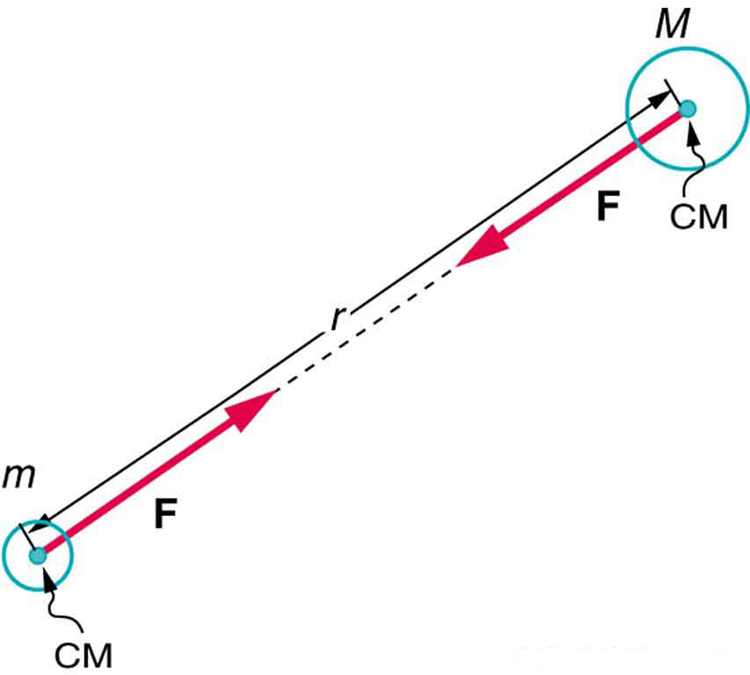
The magnitude of the force on each object (one has larger mass than the other) is the same, consistent with Newton’s third law.
The bodies we are dealing with tend to be large. To simplify the situation we assume that the body acts as if its entire mass is concentrated at one specific point called the center of mass (CM), which will be further explored in Linear Momentum and Collisions . For two bodies having masses and with a distance between their centers of mass, the equation for Newton’s universal law of gravitation is
where is the magnitude of the gravitational force and is a proportionality factor called the gravitational constant . is a universal gravitational constant—that is, it is thought to be the same everywhere in the universe. It has been measured experimentally to be
in SI units. Note that the units of are such that a force in newtons is obtained from , when considering masses in kilograms and distance in meters. For example, two 1.000 kg masses separated by 1.000 m will experience a gravitational attraction of . This is an extraordinarily small force. The small magnitude of the gravitational force is consistent with everyday experience. We are unaware that even large objects like mountains exert gravitational forces on us. In fact, our body weight is the force of attraction of the entire Earth on us with a mass of .
Recall that the acceleration due to gravity is about on Earth. We can now determine why this is so. The weight of an object mg is the gravitational force between it and Earth. Substituting mg for in Newton’s universal law of gravitation gives
where is the mass of the object, is the mass of Earth, and is the distance to the center of Earth (the distance between the centers of mass of the object and Earth). See [link] . The mass of the object cancels, leaving an equation for :
Substituting known values for Earth’s mass and radius (to three significant figures),
and we obtain a value for the acceleration of a falling body:
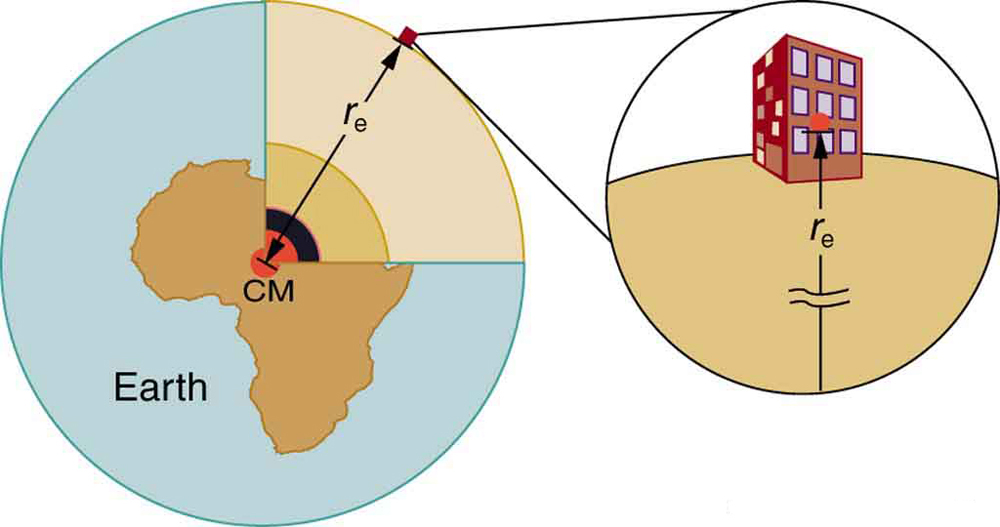
This is the expected value and is independent of the body’s mass . Newton’s law of gravitation takes Galileo’s observation that all masses fall with the same acceleration a step further, explaining the observation in terms of a force that causes objects to fall—in fact, in terms of a universally existing force of attraction between masses.
Take a marble, a ball, and a spoon and drop them from the same height. Do they hit the floor at the same time? If you drop a piece of paper as well, does it behave like the other objects? Explain your observations.

Notification Switch
Would you like to follow the 'Introduction to applied math and physics' conversation and receive update notifications?