5.3 Newton's 3rd law

There is a passage in the musical Man of la Mancha that relates to Newton’s third law of motion. Sancho, in describing a fight with his wife to Don Quixote, says, “Of course I hit her back, Your Grace, but she’s a lot harder than me and you know what they say, ‘Whether the stone hits the pitcher or the pitcher hits the stone, it’s going to be bad for the pitcher.’” This is exactly what happens whenever one body exerts a force on another—the first also experiences a force (equal in magnitude and opposite in direction). Numerous common experiences, such as stubbing a toe or throwing a ball, confirm this. It is precisely stated in Newton’s third law of motion    .

This law represents a certain symmetry in nature : Forces always occur in pairs, and one body cannot exert a force on another without experiencing a force itself. We sometimes refer to this law loosely as “action-reaction,” where the force exerted is the action and the force experienced as a consequence is the reaction. Newton’s third law has practical uses in analyzing the origin of forces and understanding which forces are external to a system.

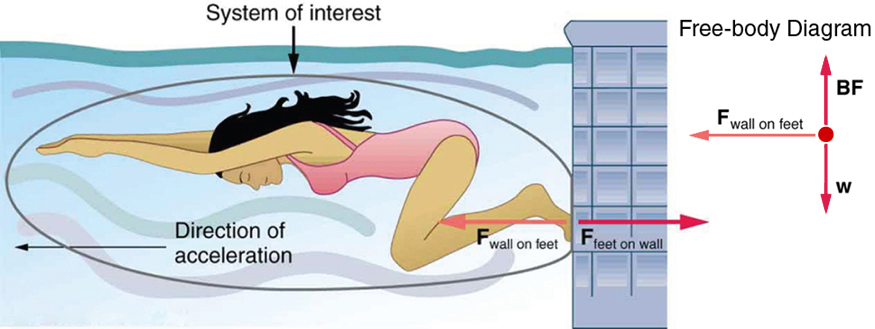
We can readily see Newton’s third law at work by taking a look at how people move about. Consider a swimmer pushing off from the side of a pool, as illustrated in [link] . She pushes against the pool wall with her feet and accelerates in the direction opposite to that of her push. The wall has exerted an equal and opposite force back on the swimmer. You might think that two equal and opposite forces would cancel, but they do not because they act on different systems . In this case, there are two systems that we could investigate: the swimmer or the wall. If we select the swimmer to be the system of interest, as in the figure, then ${\mathbf{\text{F}}}_{\text{wall on feet}}$ is an external force on this system and affects its motion. The swimmer moves in the direction of ${\mathbf{\text{F}}}_{\text{wall on feet}}$ . In contrast, the force ${\mathbf{\text{F}}}_{\text{feet on wall}}$ acts on the wall and not on our system of interest. Thus ${\mathbf{\text{F}}}_{\text{feet on wall}}$ does not directly affect the motion of the system and does not cancel ${\mathbf{\text{F}}}_{\text{wall on feet}}$ . Note that the swimmer pushes in the direction opposite to that in which she wishes to move. The reaction to her push is thus in the desired direction.