5.2 Graphical analysis of one-dimensional motion  (Page 2/8)

Graphs of motion when $a$ Is constant but

The graphs in [link] below represent the motion of the jet-powered car as it accelerates toward its top speed, but only during the time when its acceleration is constant. Time starts at zero for this motion (as if measured with a stopwatch), and the displacement and velocity are initially 200 m and 15 m/s, respectively.

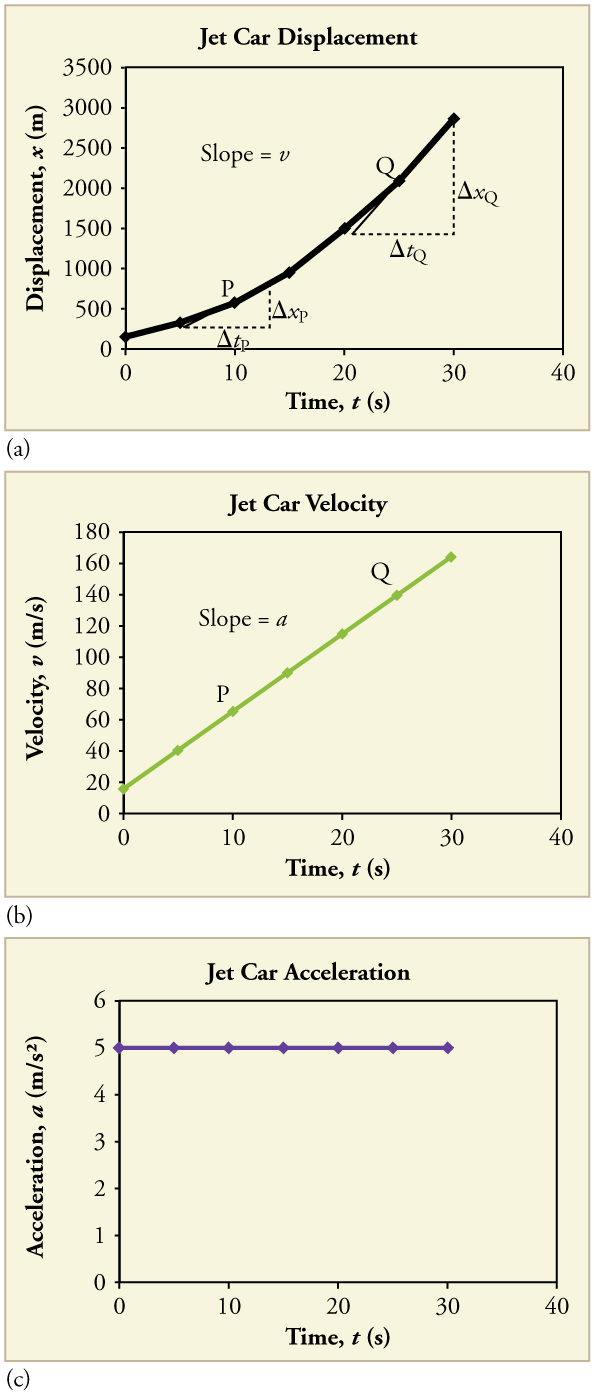
The graph of displacement versus time in [link] (a) is a curve rather than a straight line. The slope of the curve becomes steeper as time progresses, showing that the velocity is increasing over time. The slope at any point on a displacement-versus-time graph is the instantaneous velocity at that point. It is found by drawing a straight line tangent to the curve at the point of interest and taking the slope of this straight line. Tangent lines are shown for two points in [link] (a). If this is done at every point on the curve and the values are plotted against time, then the graph of velocity versus time shown in [link] (b) is obtained. Furthermore, the slope of the graph of velocity versus time is acceleration, which is shown in [link] (c).

Determining instantaneous velocity from the slope at a point: jet car

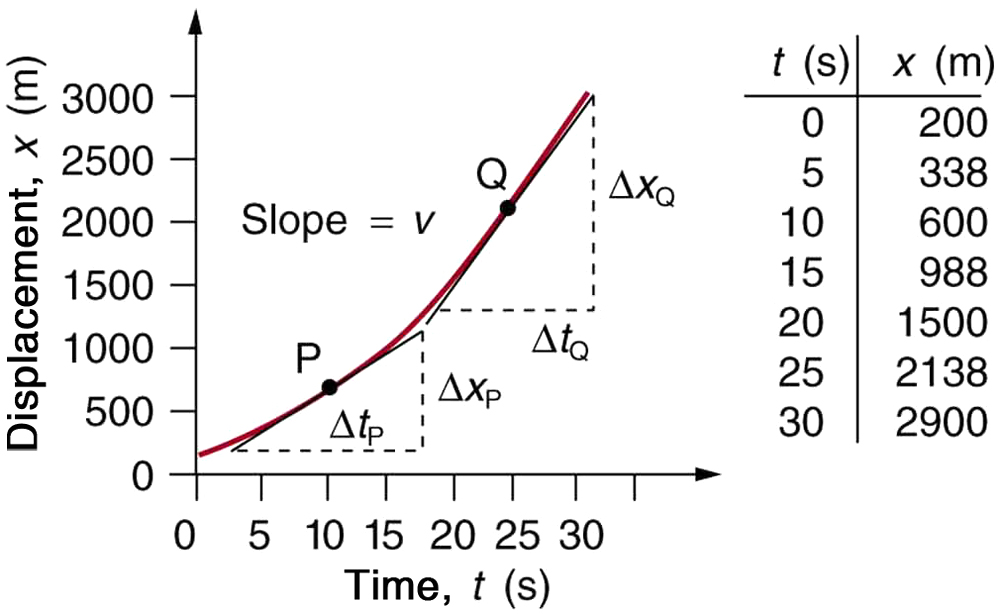
Calculate the velocity of the jet car at a time of 25 s by finding the slope of the $x$ vs. $t$ graph in the graph below.

Strategy

The slope of a curve at a point is equal to the slope of a straight line tangent to the curve at that point. This principle is illustrated in [link] , where Q is the point at $t=\text{25 s}$ .

Solution

1. Find the tangent line to the curve at $t=\text{25 s}$ .

2. Determine the endpoints of the tangent. These correspond to a position of 1300 m at time 19 s and a position of 3120 m at time 32 s.

3. Plug these endpoints into the equation to solve for the slope, $v$ .

$\text{slope}=v_{\mathrm{Q}}=\frac{{\mathrm{\Delta }x}_{\mathrm{Q}}}{{\mathrm{\Delta }t}_{\mathrm{Q}}}=\frac{\left(\text{3120 m}-\text{1300 m}\right)}{\left(\text{32 s}-\text{19 s}\right)}$

Thus,

$v_{\mathrm{Q}}=\frac{\text{1820 m}}{\text{13 s}}=\text{140 m/s.}$

Discussion

This is the value given in this figure’s table for $v$ at $t=\text{25 s}$ . The value of 140 m/s for $v_{\mathrm{Q}}$ is plotted in [link] . The entire graph of $v$ vs. $t$ can be obtained in this fashion.

Carrying this one step further, we note that the slope of a velocity versus time graph is acceleration. Slope is rise divided by run; on a $v$ vs. $t$ graph, rise = change in velocity $\mathrm{\Delta }v$ and run = change in time $\mathrm{\Delta }t$ .

Since the velocity versus time graph in [link] (b) is a straight line, its slope is the same everywhere, implying that acceleration is constant. Acceleration versus time is graphed in [link] (c).