5.15 Discrete-time filtering of analog signals

Because of the Sampling Theorem , we can process, in particular filter, analog signals "with a computer" by constructing the system shown in [link] . To use this system, we are assuming that the input signal has a lowpass spectrum andcan be bandlimited without affecting important signal aspects. Bandpass signals can also be filtered digitally, but require amore complicated system. Highpass signals cannot be filtered digitally. Note that the input and output filters must be analogfilters; trying to operate without them can lead to potentially very inaccurate digitization.

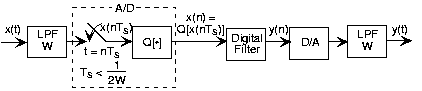
Another implicit assumption is that the digital filter can operate in real time : The computer and the filtering algorithm must be sufficiently fast so that outputs are computedfaster than input values arrive. The sampling interval, which is determined by the analog signal's bandwidth, thus determines how longour program has to compute each output $y(n)$ . The computational complexity for calculating each output with a difference equation is $O(p+q)$ . Frequency domain implementation of the filter is also possible. The idea begins by computing the Fouriertransform of a length- $N$ portion of the input $x(n)$ , multiplying it by the filter's transfer function, and computing the inverse transform of the result. This approachseems overly complex and potentially inefficient. Detailing the complexity, however, we have $O(N\lg N)$ for the two transforms (computed using the FFT algorithm) and $O(N)$ for the multiplication by the transfer function, which makes the total complexity $O(N\lg N)$ for $N$ input values . A frequency domain implementation thus requires $O(\lg N)$ computational complexity for each output value. The complexities of time-domain and frequency-domain implementations depend ondifferent aspects of the filtering: The time-domain implementation depends on the combined orders of the filterwhile the frequency-domain implementation depends on the logarithm of the Fourier transform's length.

It could well be that in some problems the time-domain version is more efficient (more easily satisfies the real timerequirement), while in others the frequency domain approach isfaster. In the latter situations, it is the FFT algorithm for computing the Fourier transforms that enables thesuperiority of frequency-domain implementations. Because complexity considerations only express how algorithm running-time increaseswith system parameter choices, we need to detail both implementations to determine which will be more suitable for anygiven filtering problem. Filtering with a difference equation is straightforward, and the number of computations that must bemade for each output value is $2(p+q)$ .