5.1 Kinematics in two dimensions: an introduction  (Page 2/3)

The independence of perpendicular motions

The person taking the path shown in [link] walks east and then north (two perpendicular directions). How far he or she walks east is only affected by his or her motion eastward. Similarly, how far he or she walks north is only affected by his or her motion northward.

This is true in a simple scenario like that of walking in one direction first, followed by another. It is also true of more complicated motion involving movement in two directions at once. For example, let’s compare the motions of two baseballs. One baseball is dropped from rest. At the same instant, another is thrown horizontally from the same height and follows a curved path. A stroboscope has captured the positions of the balls at fixed time intervals as they fall.

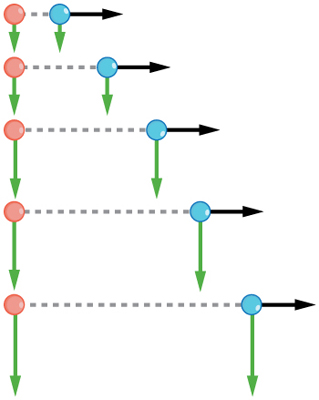
It is remarkable that for each flash of the strobe, the vertical positions of the two balls are the same. This similarity implies that the vertical motion is independent of whether or not the ball is moving horizontally. (Assuming no air resistance, the vertical motion of a falling object is influenced by gravity only, and not by any horizontal forces.) Careful examination of the ball thrown horizontally shows that it travels the same horizontal distance between flashes. This is due to the fact that there are no additional forces on the ball in the horizontal direction after it is thrown. This result means that the horizontal velocity is constant, and affected neither by vertical motion nor by gravity (which is vertical). Note that this case is true only for ideal conditions. In the real world, air resistance will affect the speed of the balls in both directions.

The two-dimensional curved path of the horizontally thrown ball is composed of two independent one-dimensional motions (horizontal and vertical). The key to analyzing such motion, called projectile motion , is to resolve (break) it into motions along perpendicular directions. Resolving two-dimensional motion into perpendicular components is possible because the components are independent. We shall see how to resolve vectors in Vector Addition and Subtraction: Graphical Methods and Vector Addition and Subtraction: Analytical Methods . We will find such techniques to be useful in many areas of physics.

Phet explorations: ladybug motion 2d

Learn about position, velocity and acceleration vectors. Move the ladybug by setting the position, velocity or acceleration, and see how the vectors change. Choose linear, circular or elliptical motion, and record and playback the motion to analyze the behavior.

Summary

• The shortest path between any two points is a straight line. In two dimensions, this path can be represented by a vector with horizontal and vertical components.
• The horizontal and vertical components of a vector are independent of one another. Motion in the horizontal direction does not affect motion in the vertical direction, and vice versa.