| << Chapter < Page | Chapter >> Page > |

Figure 3 shows the buffer after M samples have been received. Note that there is no need to shift data in the buffer. The shaded area is what is being used for the fitler.

Figure 4 shows the buffer when the new sample is stored in the last element of the buffer. At this point the shifting of the data is needed to remove old data. The old data is at the beginning of the buffer. This data is just overwritten with the data at the end of the buffer.
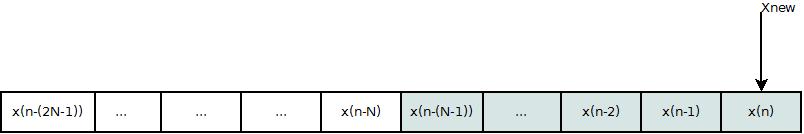
Figure 5 shows the buffer after the data has been copied. The algorithm will now use the data at the beginning of the buffer just as it did in figure 2. Notice that a large block of data is copied at one time.

The following pseudo-code shows how to implement the FIR filter using the double size FIFO type buffer. In the code the following definitions are used:
N - number of coefficients
h(n) - filter coefficients, n = 0...N-1
x(n) - stored input data, n = 0...2N-1
input_sample - variable that contains the newest input sample
index - variable that contains the current place where the new sample is to be stored
x[index] = input_sample// Filter the data
ynew = 0;for(i=0;i<N;i++){
ynew = ynew + h(i)*x(index-i);}
// update the index and copy the data if necessaryindex = index+1;
if(index>=2*N){
for (i=N-2; i>=0; i--){
x[i+N+1]= x[i];}
index = N - 1;}
The second method for storing input data is use a circular buffer. To do this you will need to keep track of an index that tells where the last input was stored. This index is incremented and used to store the new value. When the index reaches the end of the array it is wrapped around to the beginning of the array. If this method is used then the FIR algorithm is
where is modulo- N . This assumes that the index is incremented as new data is stored in the buffer. The following figure shows how the data for x ( n ) is stored in a circular buffer.
When implementing the FIR filter using a circular buffer, notice that the coefficient buffer indexes going forward and the data buffer indexes going backward.
N - number of coefficients
h(n) - filter coefficients, n = 0...N-1
x(n) - stored input data, n = 0...2N-1
input_sample - variable that contains the newest input sample
index - variable that contains the current place where the new sample is to be stored
x[index] = input_sample// Filter the data
ynew = 0;for(i=0;i<N;i++){
if((index-i)<0){
ynew = ynew + h[i]*x[index-i+N];}
else {ynew = ynew + h[i]*x[index-i];
}}
index = (index+1)%N;
In the previous implementation of the circular buffer notice that there is an if statement in the filter loop. This is very time consuming. So to remove this from the loop a buffer that is twice the length can be used. The new value that is received is put in two places within the buffer.
In the following figure shows a buffer for a circular buffer of size 4. Therefore the total length of the buffer is 8. The two indexes point to the places where the input sample is stored. In the figure the shaded boxes are the intems that make up the filter elements. Since the samples do not wrap around the end of the buffer there is no need to check the offset in the loop.

After the filter output is determine the indexes are incremented and checked to see if they go past the end of the buffer. The following figure shows the buffer and indexes after one increment.

The following figure shows the indexes after another increment. Notice that the indexes wrap around and the element that are used still don't wrap around the end of the buffer.

To implement the double size circular buffer the following pseudo-code can be used.
N - number of coefficients
h(n) - filter coefficients, n = 0...N-1
x(n) - stored input data, n = 0...2N-1
input_sample - variable that contains the newest input sample
index1 - the first place in x(n) where the new sample is to be stored
index2 - the second place in x(n) where the new sample is to be stored
// variable are initialized to the following values
int index1=0;int index2=N;// As a new sample is received put it in two places
x[index1]= input_sample;
x[index2]= input_sample;
ynew = 0;for(i=0;i<N;i++){
ynew = ynew + h[i]*x[index2-i];}
index1 = (index1+1)%N;index2 = index1+N;

Notification Switch
Would you like to follow the 'Dsp lab with ti c6x dsp and c6713 dsk' conversation and receive update notifications?