5.1 Double integrals over rectangular regions  (Page 8/12)

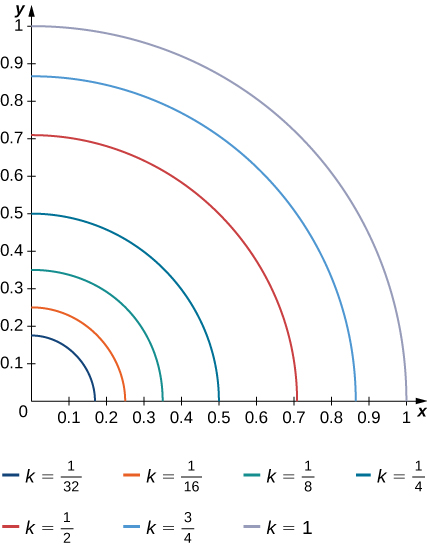
The level curves $f(x,y)=k$ of the function f are given in the following graph, where k is a constant.

1. Apply the midpoint rule with $m=n=2$ to estimate the double integral ${\displaystyle \underset{R}{\iint }f(x,y)dA},$ where $R=[0.1,0.5]\times [0.1,0.5].$
2. Estimate the average value of the function f on R .
   

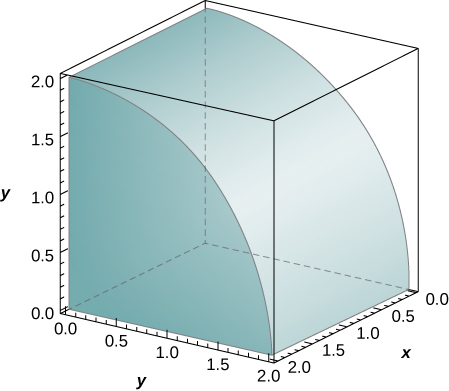
The solid lying under the surface $z=\sqrt{4-y^2}$ and above the rectangular region $R=[0,2]\times \left[0,2\right]$ is illustrated in the following graph. Evaluate the double integral ${\displaystyle \underset{R}{\iint }f(x,y)dA},$ where $f(x,y)=\sqrt{4-y^2},$ by finding the volume of the corresponding solid.

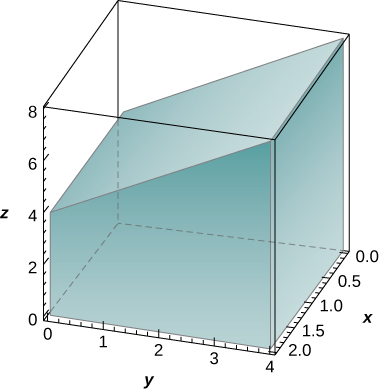
The solid lying under the plane $z=y+4$ and above the rectangular region $R=[0,2]\times \left[0,4\right]$ is illustrated in the following graph. Evaluate the double integral ${\displaystyle \underset{R}{\iint }f(x,y)dA},$ where $f(x,y)=y+4,$ by finding the volume of the corresponding solid.

${\displaystyle \underset{\mathrm{-1}}{\overset{1}{\int }}\left({\displaystyle \underset{\mathrm{-2}}{\overset{2}{\int }}\left(2x+3y+5\right)dx}\right)}dy$

${\displaystyle \underset{0}{\overset{2}{\int }}\left({\displaystyle \underset{0}{\overset{1}{\int }}\left(x+2e^y-3\right)dx}\right)}dy$

${\displaystyle \underset{1}{\overset{27}{\int }}\left({\displaystyle \underset{1}{\overset{2}{\int }}\left(\sqrt[3]{x}+\sqrt[3]{y}\right)}dy\right)dx}$

${\displaystyle \underset{1}{\overset{16}{\int }}\left({\displaystyle \underset{1}{\overset{8}{\int }}\left(\sqrt[4]{x}+2\sqrt[3]{y}\right)}dy\right)dx}$

${\displaystyle \underset{\text{ln}2}{\overset{\text{ln}3}{\int }}\left({\displaystyle \underset{0}{\overset{\mathrm{l}}{\int }}{e}^{x+y}dy}\right)}dx$

${\displaystyle \underset{0}{\overset{2}{\int }}\left({\displaystyle \underset{0}{\overset{1}{\int }}{3}^{x+y}dy}\right)}dx$

${\displaystyle \underset{1}{\overset{6}{\int }}\left({\displaystyle \underset{2}{\overset{9}{\int }}\frac{\sqrt{y}}{x^2}}dy\right)}dx$

${\displaystyle \underset{1}{\overset{9}{\int }}\left({\displaystyle \underset{4}{\overset{2}{\int }}\frac{\sqrt{x}}{y^2}}dy\right)}dx$

${\displaystyle \underset{0}{\overset{\pi }{\int }}{\displaystyle \underset{0}{\overset{\pi \text{/}2}{\int }}\text{sin}(2x)\text{cos}(3y)}}dxdy$

${\displaystyle \underset{\pi \text{/}12}{\overset{\pi \text{/}8}{\int }}{\displaystyle \underset{\pi \text{/}4}{\overset{\pi \text{/}3}{\int }}\left[\text{cot}x+\text{tan}(2y)\right]}}dxdy$

${\displaystyle \underset{1}{\overset{e}{\int }}{\displaystyle \underset{1}{\overset{e}{\int }}\left[\frac{1}{x}\text{sin}(\text{ln}x)+\frac{1}{y}\text{cos}(\text{ln}y)\right]dxdy}}$

${\displaystyle \underset{1}{\overset{e}{\int }}{\displaystyle \underset{1}{\overset{e}{\int }}\frac{\text{sin}(\text{ln}x)\text{cos}(\text{ln}y)}{xy}dxdy}}$

${\displaystyle \underset{1}{\overset{2}{\int }}{\displaystyle \underset{1}{\overset{2}{\int }}\left(\frac{\text{ln}y}{x}+\frac{x}{2y+1}\right)}}dydx$

${\displaystyle \underset{1}{\overset{e}{\int }}{\displaystyle \underset{1}{\overset{2}{\int }}{x}^2\text{ln}(x)}}dydx$

${\displaystyle \underset{1}{\overset{\sqrt{3}}{\int }}{\displaystyle \underset{1}{\overset{2}{\int }}y\text{arctan}\left(\frac{1}{x}\right)}}dydx$

${\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{0}{\overset{1\text{/}2}{\int }}\left(\text{arcsin}x+\text{arcsin}y\right)}}dydx$

${\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{1}{\overset{2}{\int }}x{e}^{x+4y}}}dydx$

${\displaystyle \underset{1}{\overset{2}{\int }}{\displaystyle \underset{0}{\overset{1}{\int }}x{e}^{x-y}}}dydx$

${\displaystyle \underset{1}{\overset{e}{\int }}{\displaystyle \underset{1}{\overset{e}{\int }}\left(\frac{\text{ln}y}{\sqrt{y}}+\frac{\text{ln}x}{\sqrt{x}}\right)}}dydx$

${\displaystyle \underset{1}{\overset{e}{\int }}{\displaystyle \underset{1}{\overset{e}{\int }}\left(\frac{x\text{ln}y}{\sqrt{y}}+\frac{y\text{ln}x}{\sqrt{x}}\right)}}dydx$

${\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{1}{\overset{2}{\int }}\left(\frac{x}{x^2+y^2}\right)}}dydx$

${\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{1}{\overset{2}{\int }}\frac{y}{x+y^2}}}dydx$

$f(x,y)=\text{−}x+2y,$ $R=[0,1]\times \left[0,1\right]$

$f(x,y)=x^4+2y^3,$ $R=[1,2]\times \left[2,3\right]$

$f(x,y)=\text{sinh}x+\text{sinh}y,$ $R=[0,1]\times \left[0,2\right]$

$f(x,y)=\text{arctan}(xy),$ $R=\left[0,1\right]\times \left[0,1\right]$

Let f and g be two continuous functions such that $0\le m_1\le f(x)\le M_1$ for any $x\in [a,b]$ and $0\le m_2\le g(y)\le M_2$ for any $y\in [c,d].$ Show that the following inequality is true:

$m_1{m}_2(b-a)(c-d)\le {\displaystyle \underset{a}{\overset{b}{\int }}{\displaystyle \underset{c}{\overset{d}{\int }}f(x)g(y)dydx}}\le M_1{M}_2(b-a)(c-d).$

$\frac{1}{e^2}\le {\displaystyle \underset{R}{\iint }{e}^{\text{−}{x}^2-y^2}dA}\le 1,$ where $R=\left[0,1\right]\times \left[0,1\right]$

$\frac{{\pi }^2}{144}\le {\displaystyle \underset{R}{\iint }\text{sin}x\text{cos}ydA}\le \frac{{\pi }^2}{48},$ where $R=\left[\frac{\pi }{6},\frac{\pi }{3}\right]\times \left[\frac{\pi }{6},\frac{\pi }{3}\right]$

$0\le {\displaystyle \underset{R}{\iint }{e}^{\text{−}y}\text{cos}xdA}\le \frac{\pi }{2},$ where $R=\left[0,\frac{\pi }{2}\right]\times \left[0,\frac{\pi }{2}\right]$

$0\le {\displaystyle \underset{R}{\iint }\left(\text{ln}x\right)\left(\text{ln}y\right)dA}\le {\left(e-1\right)}^2,$ where $R=\left[1,e\right]\times \left[1,e\right]$

Let f and g be two continuous functions such that $0\le m_1\le f(x)\le M_1$ for any $x\in [a,b]$ and $0\le m_2\le g(y)\le M_2$ for any $y\in [c,d].$ Show that the following inequality is true:

$\left(m_1+m_2\right)(b-a)(c-d)\le {\displaystyle \underset{a}{\overset{b}{\int }}{\displaystyle \underset{c}{\overset{d}{\int }}\left[f(x)+g(y)\right]dydx}}\le \left(M_1+M_2\right)(b-a)(c-d).$

$\frac{2}{e}\le {\displaystyle \underset{R}{\iint }\left(e^{\text{−}{x}^2}+e^{\text{−}{y}^2}\right)dA}\le 2,$ where $R=\left[0,1\right]\times \left[0,1\right]$

$\frac{{\pi }^2}{36}\le {\displaystyle \underset{R}{\iint }\left(\text{sin}x+\text{cos}y\right)}dA\le \frac{{\pi }^2\sqrt{3}}{36},$ where $R=\left[\frac{\pi }{6},\frac{\pi }{3}\right]\times \left[\frac{\pi }{6},\frac{\pi }{3}\right]$

$\frac{\pi }{2}{e}^{\text{−}\pi \text{/}2}\le {\displaystyle \underset{R}{\iint }\left(\text{cos}x+e^{\text{−}y}\right)}dA\le \pi ,$ where $R=\left[0,\frac{\pi }{2}\right]\times \left[0,\frac{\pi }{2}\right]$

$\frac{1}{e}\le {\displaystyle \underset{R}{\iint }\left(e^{\text{−}y}-\text{ln}x\right)}dA\le 2,$ where $R=\left[0,1\right]\times \left[0,1\right]$

[T] $f(x,y)={\displaystyle \underset{0}{\overset{y}{\int }}{\displaystyle \underset{0}{\overset{x}{\int }}(xs+yt)dsdt}},$ where $(x,y)\in R=[0,1]\times [0,1]$

[T] $f(x,y)={\displaystyle \underset{0}{\overset{x}{\int }}{\displaystyle \underset{0}{\overset{y}{\int }}\left[\text{cos}\left(s\right)+\text{cos}\left(t\right)\right]dtds}},$ where $(x,y)\in R=[0,3]\times [0,3]$

Show that if f and g are continuous on $[a,b]$ and $[c,d],$ respectively, then

${\displaystyle \underset{a}{\overset{b}{\int }}{\displaystyle \underset{c}{\overset{d}{\int }}\left[f(x)+g(y)\right]dydx}}=(d-c){\displaystyle \underset{a}{\overset{b}{\int }}f(x)dx}$

$+{\displaystyle \underset{a}{\overset{b}{\int }}{\displaystyle \underset{c}{\overset{d}{\int }}g(y)dy}}dx=(b-a){\displaystyle \underset{c}{\overset{d}{\int }}g(y)dy+}{\displaystyle \underset{c}{\overset{d}{\int }}{\displaystyle \underset{a}{\overset{b}{\int }}f(x)dx}}dy.$

Show that ${\displaystyle \underset{a}{\overset{b}{\int }}{\displaystyle \underset{c}{\overset{d}{\int }}yf(x)+xg(y)dydx}}=\frac{1}{2}\left(d^2-c^2\right)\left({\displaystyle \underset{a}{\overset{b}{\int }}f(x)dx}\right)+\frac{1}{2}\left(b^2-a^2\right)\left({\displaystyle \underset{c}{\overset{d}{\int }}g(y)dy}\right).$

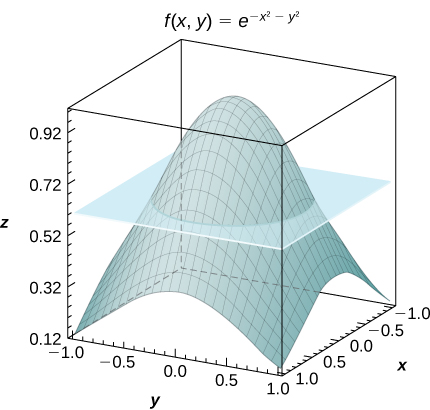
[T] Consider the function $f(x,y)=e^{\text{−}{x}^2-y^2},$ where $(x,y)\in R=[\mathrm{-1},1]\times [\mathrm{-1},1].$

1. Use the midpoint rule with $m=n=2,4\text{,…,}10$ to estimate the double integral $I={\displaystyle \underset{R}{\iint }{e}^{\text{−}{x}^2-y^2}dA}.$ Round your answers to the nearest hundredths.
2. For $m=n=2,$ find the average value of f over the region R . Round your answer to the nearest hundredths.
3. Use a CAS to graph in the same coordinate system the solid whose volume is given by ${\displaystyle \underset{R}{\iint }{e}^{\text{−}{x}^2-y^2}dA}$ and the plane $z=f_{\text{ave}}.$

[T] Consider the function $f(x,y)=\text{sin}\left(x^2\right)\text{cos}\left(y^2\right),$ where $(x,y)\in R=[\mathrm{-1},1]\times [\mathrm{-1},1].$

1. Use the midpoint rule with $m=n=2,4\text{,…,}10$ to estimate the double integral $I={\displaystyle \underset{R}{\iint }\text{sin}\left(x^2\right)\text{cos}\left(y^2\right)dA}.$ Round your answers to the nearest hundredths.
2. For $m=n=2,$ find the average value of f over the region R. Round your answer to the nearest hundredths.
3. Use a CAS to graph in the same coordinate system the solid whose volume is given by ${\displaystyle \underset{R}{\iint }\text{sin}\left(x^2\right)\text{cos}\left(y^2\right)dA}$ and the plane $z=f_{\text{ave}}.$

$f(x,y)=x^n+y^n+xy,(x,y)\in R=[0,1]\times [0,1]$

$f(x,y)=\frac{1}{x^n}+\frac{1}{y^n},(x,y)\in R=[1,2]\times [1,2]$

Show that the average value of a function f on a rectangular region $R=[a,b]\times [c,d]$ is $f_{\text{ave}}\approx \frac{1}{mn}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^{n}f\left(x_{ij}^{*},y_{ij}^{*}\right)}},$ where $\left(x_{ij}^{*},y_{ij}^{*}\right)$ are the sample points of the partition of R , where $1\le i\le m$ and $1\le j\le n.$

Use the midpoint rule with $m=n$ to show that the average value of a function f on a rectangular region $R=[a,b]\times [c,d]$ is approximated by

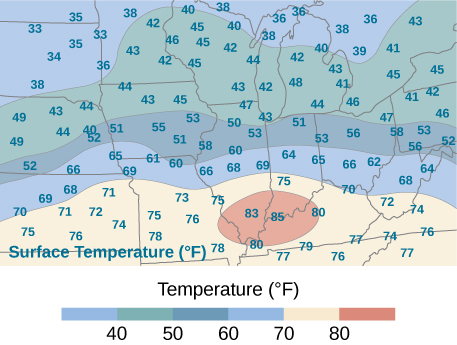
An isotherm map is a chart connecting points having the same temperature at a given time for a given period of time. Use the preceding exercise and apply the midpoint rule with $m=n=2$ to find the average temperature over the region given in the following figure.