| << Chapter < Page | Chapter >> Page > |
A rocket is accelerating straight up. Its engines produce of thrust, and air resistance is . What is the rocket’s acceleration? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
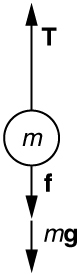
Using the free-body diagram:
,
so that
.
The wheels of a midsize car exert a force of 2100 N backward on the road to accelerate the car in the forward direction. If the force of friction including air resistance is 250 N and the acceleration of the car is , what is the mass of the car plus its occupants? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion. For this situation, draw a free-body diagram and write the net force equation.
Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
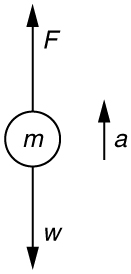
Find: .
. The force exerted by the high-jumper is actually down on the ground, but is up from the ground and makes him jump.
When landing after a spectacular somersault, a 40.0-kg gymnast decelerates by pushing straight down on the mat. Calculate the force she must exert if her deceleration is 7.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
A freight train consists of two engines and 45 cars with average masses of . (a) What force must each engine exert backward on the track to accelerate the train at a rate of if the force of friction is , assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems. (b) What is the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?
(a)
(b)
Commercial airplanes are sometimes pushed out of the passenger loading area by a tractor. (a) An 1800-kg tractor exerts a force of backward on the pavement, and the system experiences forces resisting motion that total 2400 N. If the acceleration is , what is the mass of the airplane? (b) Calculate the force exerted by the tractor on the airplane, assuming 2200 N of the friction is experienced by the airplane. (c) Draw two sketches showing the systems of interest used to solve each part, including the free-body diagrams for each.

Notification Switch
Would you like to follow the 'Introduction to applied math and physics' conversation and receive update notifications?