| << Chapter < Page | Chapter >> Page > |
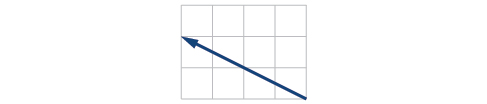
Given initial point and terminal point write the vector in terms of and then draw the vector on the graph.
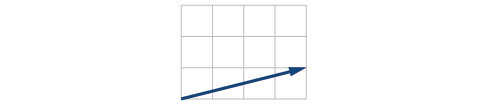
Given initial point and terminal point write the vector in terms of and Draw the points and the vector on the graph.
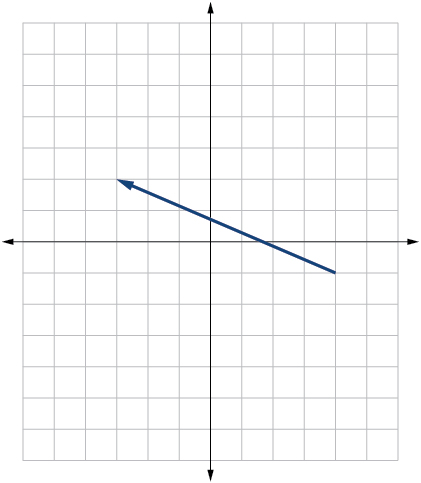
Given initial point and terminal point write the vector in terms of and Draw the points and the vector on the graph.
For the following exercises, use the given magnitude and direction in standard position, write the vector in component form.
A 60-pound box is resting on a ramp that is inclined 12°. Rounding to the nearest tenth,
a. 58.7; b. 12.5
A 25-pound box is resting on a ramp that is inclined 8°. Rounding to the nearest tenth,
Find the magnitude of the horizontal and vertical components of a vector with magnitude 8 pounds pointed in a direction of 27° above the horizontal. Round to the nearest hundredth.
pounds, pounds
Find the magnitude of the horizontal and vertical components of the vector with magnitude 4 pounds pointed in a direction of 127° above the horizontal. Round to the nearest hundredth.
Find the magnitude of the horizontal and vertical components of a vector with magnitude 5 pounds pointed in a direction of 55° above the horizontal. Round to the nearest hundredth.
pounds, pounds
Find the magnitude of the horizontal and vertical components of the vector with magnitude 1 pound pointed in a direction of 8° above the horizontal. Round to the nearest hundredth.
A woman leaves home and walks 3 miles west, then 2 miles southwest. How far from home is she, and in what direction must she walk to head directly home?
4.635 miles, 17.764° N of E
A boat leaves the marina and sails 6 miles north, then 2 miles northeast. How far from the marina is the boat, and in what direction must it sail to head directly back to the marina?
A man starts walking from home and walks 4 miles east, 2 miles southeast, 5 miles south, 4 miles southwest, and 2 miles east. How far has he walked? If he walked straight home, how far would he have to walk?
17 miles. 10.318 miles
A woman starts walking from home and walks 4 miles east, 7 miles southeast, 6 miles south, 5 miles southwest, and 3 miles east. How far has she walked? If she walked straight home, how far would she have to walk?
A man starts walking from home and walks 3 miles at 20° north of west, then 5 miles at 10° west of south, then 4 miles at 15° north of east. If he walked straight home, how far would he have to the walk, and in what direction?
Distance: 2.868. Direction: 86.474° North of West, or 3.526° West of North

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?