4.7 Derivation of the fourier transform

Fourier series clearly open the frequency domain as an interesting and useful way of determining how circuits andsystems respond to periodic input signals. Can we use similar techniques for nonperiodic signals? What isthe response of the filter to a single pulse? Addressing these issues requires us to find the Fourier spectrum of all signals,both periodic and nonperiodic ones. We need a definition for the Fourier spectrum of a signal, periodic or not. This spectrum is calculated by what is known as the Fourier transform .

Let $s_T(t)$ be a periodic signal having period $T$ . We want to consider what happens to this signal's spectrum as welet the period become longer and longer. We denote the spectrum for any assumed value of the period by $c_k(T)$ . We calculate the spectrum according to the familiar formula

Spectrum

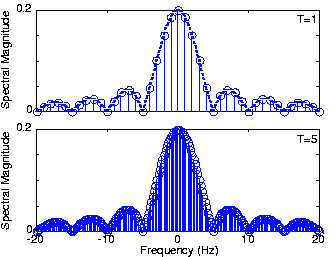
[link] shows how increasing the period does indeed lead to a continuum of coefficients, and thatthe Fourier transform does correspond to what the continuum becomes. The quantity $\frac{\sin t}{t}$ has a special name, the sinc (pronounced "sink") function, and is denoted by $\mathrm{sinc}(t)$ . Thus, the magnitude of the pulse's Fourier transform equals $\left|\Delta \mathrm{sinc}(\pi f\Delta )\right|$ .

The Fourier transform relates a signal's time and frequencydomain representations to each other. The direct Fourier transform (or simply the Fourier transform) calculates asignal's frequency domain representation from its time-domain variant ( [link] ). The inverse Fourier transform ( [link] ) finds the time-domain representation from the frequencydomain. Rather than explicitly writing the required integral, we often symbolically express these transform calculations as $ℱ(s)$ and $ℱ^{(-1)}(S)$ , respectively.