| << Chapter < Page | Chapter >> Page > |
The learners must be able to:
1. identify and solve problems and make decisions using critical and creative thinking;
2. work effectively with others as members of a team, group, organisation and community;
3. organise and manage themselves and their activities responsibly and effectively;
4. collect, analyse, organise and critically evaluate information;
5. communicate effectively using visual, symbolic and/or language skills in various modes;
6. use science and technology effectively and critically, showing responsibility towards the environment and the health of others;
6. demonstrate an understanding of the world as a set of related systems by recognising that problem-solving contexts do not exist in isolation;
7. reflect on and explore a variety of strategies to learn more effectively;
8. participate as responsible citizens in the life of local, national, and global communities;
9. be culturally and aesthetically sensitive across a range of social contexts;
10. explore education and career opportunities; and
develop entrepreneurial opportunities.
Learners can divide into groups, visit the library and do more research on the origin of our number system, the Roman numerals, etc.
Learners can do projects on Mathematics found in nature, in the classroom and in the home. They learn to work together in a team, listen to one another and to share ideas.
Discuss whether so called “bargains” are always bargains. What is your attitude towards “sales” in shops? Is it always necessary to give / receive birthday presents? Why do you give presents? When would not giving presents be acceptable?
(“History of numbers”, MacDonald’s First Library, “Number”)
Abelard was a monk who lived in the twelfth century A.D. He lived in England.
Abelard loved to solve number puzzles.
He used Roman figures such as these with which to count:
I, II, III, IV, V, VI, VII, VIII, IX, X
One day some Arab merchants told Abelard about a secret sign and nine numbers used by the Arabs for counting. They said any total could be written using nine numbers and the secret sign.
One night Abelard climbed over the wall of the monastery in England and set off to Cordova in Spain. It took him many months to get there and to learn the language. After many exciting and dangerous adventures, he returned to England bringing with him the Arabs’ secret. He used the Arabic numbers 1, 2, 3, 4, 5, 6, 7, 8 and 9 AND the “0” - the secret sign - as a placeholder. Making use of the secret sign “0” he could write any number.
The Arabs learnt much from the Hindus. So Abelard returned to England with the new numbers and the secret sign.
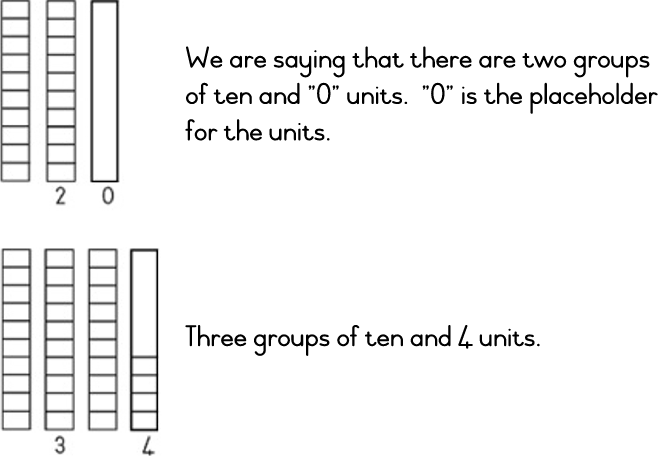
68 90
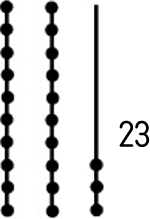
The value of 23, when renamed, is 20 + 3
The place value of the 2 in 23 is 2 tens and the place value of the 3 in 23 is 3 units.
| LO 1.5 |
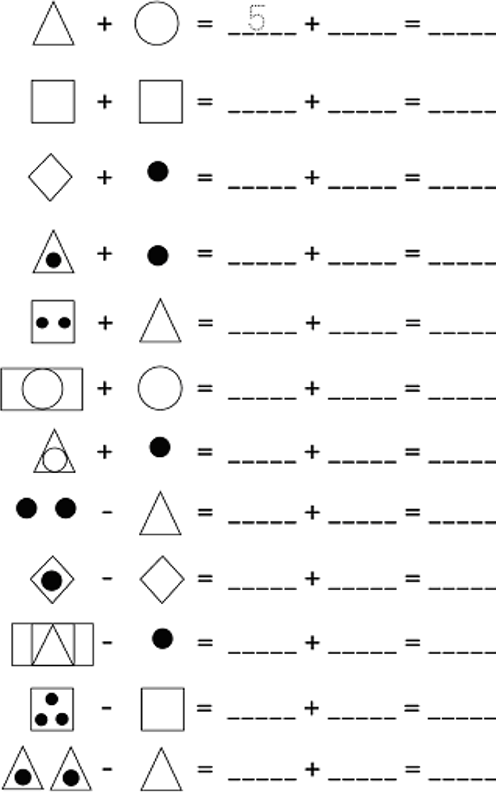
| LO 1.9 | LO 3.1 |
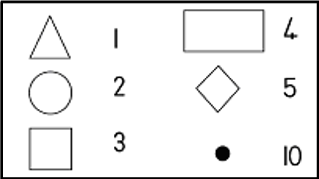
1.
2.
3.
4.
5.
6.
7.
How many were correct? _____________________________________
Name: ______________________________________________
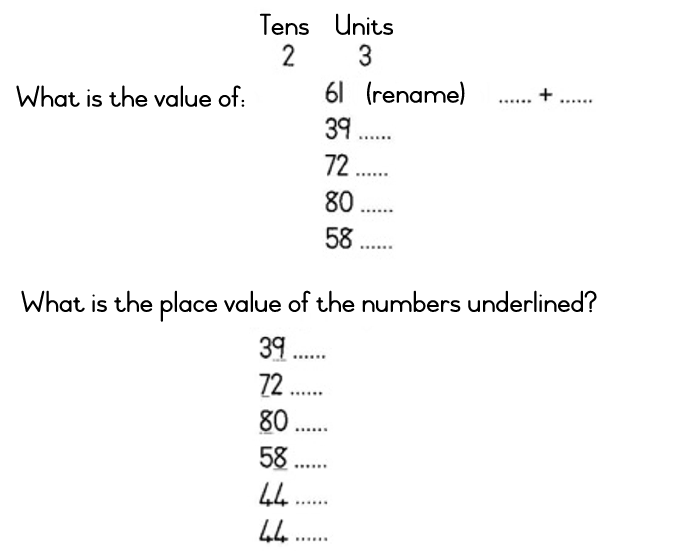
Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.5: We know this when the learner recognises the place value of digits in whole numbers to at least 2-digit numbers;
Assessment Standard 1.9: We know this when the learner performs mental calculations;
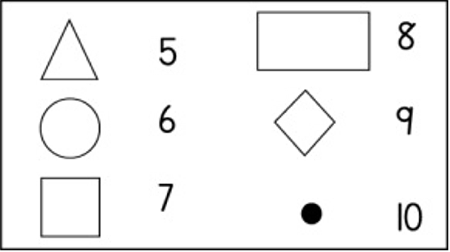
Learning Outcome 3: The learner will be able to describe and represent characteristics and relationships between two-dimensional shapes and three-dimensional objects in a variety of orientations and positions.
Assessment Standard 3.1: We know this when the learner recognises, identifies and names two-dimensional shapes and three-dimensional objects in the school environment and in pictures.
·

Notification Switch
Would you like to follow the 'Mathematics grade 2' conversation and receive update notifications?