4.6 Probability topics: tree diagrams (optional) (Page 20/3)

Collaborative statistics using Page 1 / 3

This module introduces tree diagrams as a method for making some probability problems easier to solve. This module is included in the Elementary Statistics textbook/collection as an optional lesson.

A tree diagram is a special type of graph used to determine the outcomes of an experiment. It consists of "branches" that are labeled with either frequencies or probabilities. Tree diagrams can make some probability problems easier to visualize and solve. The following example illustrates how to use a tree diagram.

In an urn, there are 11 balls. Three balls are red ( $R$ ) and 8 balls are blue ( $B$ ). Draw two balls, one at a time, with replacement . "With replacement" means that you put the first ball back in the urn before you select the second ball. The tree diagram using frequencies that show all the possible outcomes follows.

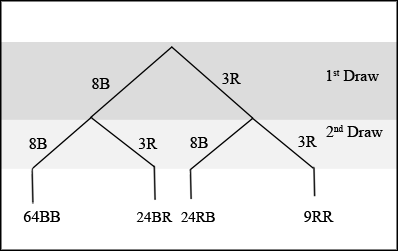
Tree diagram consisting of the first draw for the first branch and the second draw for the second branch. The first branch consists of 2 lines, 3R and 8B, and the second branch consists of 2 sets of 2 lines of 3R and 8B each. The lines produce 9RR, 24RB, 24BR, and 64BB. — $Total = 64 + 24 + 24 + 9 = 121$

The first set of branches represents the first draw. The second set of branches represents the second draw. Each of the outcomes is distinct. In fact, we can list each red ball as $R1$ , $R2$ , and $R3$ and each blue ball as $B1$ , $B2$ , $B3$ , $B4$ , $B5$ , $B6$ , $B7$ , and $B8$ . Then the 9 $RR$ outcomes can be written as:

$R1R1$
$R1R2$
$R1R3$
$R2R1$
$R2R2$
$R2R3$
$R3R1$
$R3R2$
$R3R3$

The other outcomes are similar.

There are a total of 11 balls in the urn. Draw two balls, one at a time, and with replacement. There are $11 \cdot 11 = 121$ outcomes, the size of the sample space .

List the 24 $BR$ outcomes: $B1R1$ , $B1R2$ , $B1R3$ , ...

$B1R1$
$B1R2$
$B1R3$
$B2R1$
$B2R2$
$B2R3$
$B3R1$
$B3R2$
$B3R3$
$B4R1$
$B4R2$
$B4R3$
$B5R1$
$B5R2$
$B5R3$
$B6R1$
$B6R2$
$B6R3$
$B7R1$
$B7R2$
$B7R3$
$B8R1$
$B8R2$
$B8R3$

Using the tree diagram, calculate $P(RR)$ .

$P(RR) = \frac{3}{11} \cdot \frac{3}{11} = \frac{9}{121}$

Using the tree diagram, calculate $P(RB OR BR)$ .

$P(RB OR BR) = \frac{3}{11} \cdot \frac{8}{11} + \frac{8}{11} \cdot \frac{3}{11} = \frac{48}{121}$

Using the tree diagram, calculate $P(R on 1st draw AND B on 2nd draw)$ .

$P(R on 1st draw AND B on 2nd draw) = P(RB) = \frac{3}{11} \cdot \frac{8}{11} = \frac{24}{121}$

Using the tree diagram, calculate $P(R on 2nd draw given B on 1st draw)$ .

$P(R on 2nd draw given B on 1st draw) = P(R on 2nd | B on 1st) = \frac{24}{88} = \frac{3}{11}$

This problem is a conditional. The sample space has been reduced to those outcomes that already have a blue on the first draw. There are $24 + 64 = 88$ possible outcomes (24 $BR$ and 64 $BB$ ). Twenty-four of the 88 possible outcomes are $BR$ . $\frac{24}{88} = \frac{3}{11}$ .

Using the tree diagram, calculate $P(BB)$ .

$P(BB) = \frac{64}{121}$

Using the tree diagram, calculate $P(B on the 2nd draw given R on the first draw)$ .

$P(B on 2nd draw | R on 1st draw) = \frac{8}{11}$

There are $9 + 24$ outcomes that have $R$ on the first draw (9 $RR$ and 24 $RB$ ). The sample space is then $9 + 24 = 33$ . Twenty-four of the 33 outcomes have $B$ on the second draw. The probability is then $\frac{24}{33}$ .

An urn has 3 red marbles and 8 blue marbles in it. Draw two marbles, one at a time, this time without replacement from the urn. "Without replacement" means that you do not put the first ball back before you select the second ball. Below is a tree diagram. The branches are labeled with probabilities instead of frequencies. The numbers at the ends of the branches are calculated by multiplying the numbers on the two corresponding branches, for example, $\frac{3}{11} \cdot \frac{2}{10} = \frac{6}{110}$ .

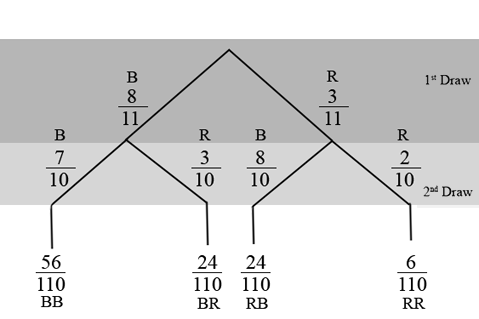
Tree diagram consisting of the first draw for the first branch and the second draw for the second branch. The first branch consists of 2 lines, B 8/11 and R 3/11, and the second branch consists of 2 sets of 2 lines with B 7/10 and R 3/10 extending from line B 8/11 and B 8/10 and R 2/10 coming from line R 3/11. These 4 lines produce BB 56/110, BR 24/110, RB 24/110, and RR 6/10. — $Total = \frac{56 + 24 + 24 + 6}{110} = \frac{110}{110} = 1$

If you draw a red on the first draw from the 3 red possibilities, there are 2 red left to draw on the second draw. You do not put back or replace the first ball after you have drawn it. You draw without replacement , so that on the second draw there are 10 marbles left in the urn.

Calculate the following probabilities using the tree diagram.

$P(RR)$ =

$P(RR) = \frac{3}{11} \cdot \frac{2}{10} = \frac{6}{110}$

Fill in the blanks:

$P(RB OR BR) = \frac{3}{11} \cdot \frac{8}{10} + (___)(___) = \frac{48}{110}$

$P(RB or BR) = \frac{3}{11} \cdot \frac{8}{10} +$ $(\frac{8}{11}) (\frac{3}{10})$ $= \frac{48}{110}$

$P(R on 2d | B on 1st)$ =

$P(R on 2d | B on 1st) = \frac{3}{10}$

Fill in the blanks:

$P(R on 1st and B on 2nd) = P(RB) = (___)(___) = \frac{24}{110}$

$P(R on 1st and B on 2nd) = P(RB) =$ $(\frac{3}{11}) (\frac{8}{10})$ $= \frac{24}{110}$

$P(BB)$ =

$P(BB) = \frac{8}{11} \cdot \frac{7}{10}$

$P(B on 2nd | R on 1st)$ =

There are $6 + 24$ outcomes that have $R$ on the first draw (6 $RR$ and 24 $RB$ ). The 6 and the 24 are frequencies. They are also the numerators of the fractions $\frac{6}{110}$ and $\frac{24}{110}$ . The sample space is no longer 110 but $6 + 24 = 30$ . Twenty-four of the 30 outcomes have $B$ on the second draw. The probability is then $\frac{24}{30}$ . Did you get this answer?

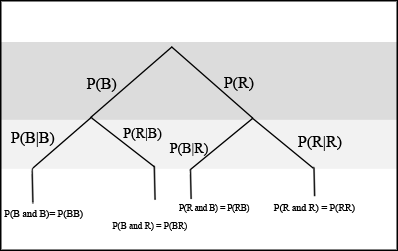
If we are using probabilities, we can label the tree in the following general way.

Tree diagram consisting of a first branch and a second branch. The first branch consists of 2 lines, P(R) and P(B), and the second branch consists of 2 sets of 2 lines with one set of P(B)(B) and P(R)(B) from line P(B) and one set of P(B)(R) and P(R)(R) from line P(R). P(B)(B) and P(R)(B) produce P(B and B)=P(BB) and P(B and R)=P(BR) and P(B)(R) and P(R)(R) produce P(R and B)=P(RB) and P(R and R)=P(RR).

$P(R|R)$ here means $P(R on 2nd | R on 1st)$
$P(B|R)$ here means $P(B on 2nd | R on 1st)$
$P(R|B)$ here means $P(R on 2nd | B on 1st)$
$P(B|B)$ here means $P(B on 2nd | B on 1st)$

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Collaborative statistics using spreadsheets. OpenStax CNX. Jan 05, 2016 Download for free at http://legacy.cnx.org/content/col11521/1.23

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Collaborative statistics using spreadsheets' conversation and receive update notifications?

Ask

	3 Lec:3 Cohort Studies By Janet Forrester Start Quiz
	9 BOD- Liver Quiz .... By Brooke Delaney Start Quiz
	Anthropology Religion Culture By Richley Crapo Start Assignment
	16 AP 16 Neurological MCQ Exam By OpenStax Start Quiz
	2 CDL Quiz - Air Brakes Endorsement Part 2 By Jazzycazz Jackson Start Quiz
	Subject-verb Agreement By Dindin Secreto Start Quiz
©flickr: Elliott	Spanish Verbs Subject Pronouns By Mariah Hauptman Start Quiz
	General Chemistry I MCQ By Joanna Smithback Start Quiz
	Pre Employment English Proficiency Exam By Katherina jennife... Start Quiz
	26 Toxicology Gustafson- Biotoxins and Venoms By Brooke Delaney Start Exam